题目内容

用一与底面成30°角的平面去截一圆柱，已知圆柱的底面半径为4，求截面椭圆的方程．
考点：平面与圆柱面的截线
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据圆柱的直径算出椭圆的短轴长，再由二面角的平面角等于30°，利用三角函数定义可算出椭圆的长轴．由此求截面椭圆的方程．
解答： 解：∵圆柱的底面半径为4，∴椭圆的短轴2b=8，得b=4
又∵椭圆所在平面与圆柱底面所成角为30°
∴cos30°=
8
2a
，可得a=
8
3
3

∴截面椭圆的方程为
x2
64
3
+
y2
16
=1．
点评：本题以一个平面截圆柱，求载得椭圆的焦距，着重考查了平面与平面所成角的含义和椭圆的简单几何性质等知识，属于基础题．
练习册系列答案
相关题目
要得到函数y=2sin2x的图象，只需将函数y=2sin（2x-
π
4
）的图象（　　）
A、向左平移
π
8
个单位
B、向右平移
π
8
个单位
C、向左平移
π
4
个单位
D、向右平移
π
4
个单位
某房地产开发公司用2.56×107元购得一块空地，计划在该空地上建造一栋至少10层，每层2000平方米的楼房，经测算，如果将楼房建为x（x≥10）层，则每平米的平均建筑费用为1000+50x（单位：元）
（Ⅰ）写出楼房平均综合费用y关于建造层数x的函数关系式；
（Ⅱ）该楼房应建造多少层时，可使楼房每平米的平均综合费用最少？最少费用是多少？（注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=
购地总费用
建筑面积
）
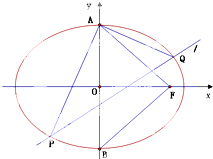如图所示，A、B分别是椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的上、下顶点，椭圆C的焦点F与抛物线y2=4
2
x的焦点重合，且S△ABF=
2
．
（1）求椭圆的方程；
（2）若不过点A的直线l与椭圆相交于P、Q两点，且AP⊥AQ，求证：直线l过定点．
某同学参加高二学业水平测试的4门必修科目考试．已知该同学每门学科考试成绩达到“A”等级的概率均为
2
3
，且每门考试成绩的结果互不影响．
（1）求该同学至少得到两个“A”的概率；
（2）已知在高考成绩计分时，每有一科达到“A”，则高考成绩加1分，如果4门学科均达到“A”，则高考成绩额外再加1分．现用随机变量Y表示该同学学业水平测试的总加分，求Y的概率分别列和数学期望．
已知函数f（x）=x3-
3
（a+1）x2+3ax．
（1）若函数f（x）在x=1处取得极值，求函数f（x）的解析式；
（2）若函数f（x）在（-∞，+∞）不单调，求实数a的取值范围；
（3）在（1）的条件下，判断过点A（1，-
5
2
）可作曲线y=f（x）多少条切线，并说明理由．
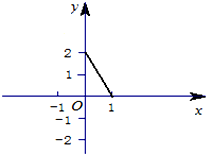已知函数y=f（x）是定义在[-1，1]上的奇函数，当x∈（0，1]时的图象如图所示．
（1）画出函数在[-1，0）上的图象；
（2）求函数y=f（x）的解析式．
已知椭圆C的极坐标方程为ρ2=
12
3cos2θ+4sin2θ
，点F1，F2为其左右焦点．以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
x=2+
2
2
t
y=
2
2
t
（t为参数，t∈R）．
（1）求直线l的普通方程和椭圆C的直角坐标方程；
（2）求点F1，F2到直线l的距离之和．
在△ABC中，角A，B，C的对边分别为a，b，c，且a＜b＜c，
a
sinA
=
2b
3
．
（1）求角B的大小；
（2）若a=2，c=3，求b边的长和△ABC的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网