题目内容
12.已知圆C过坐标原点O,且与x轴、y轴分别交于点A、B,圆心坐标为(t,t)(t>0).(1)若△AOB的面积为2,求圆C的方程;
(2)直线2x+y-6=0与圆C交于点D、E,是否存在t使得|OD|=|OE|?若存在,求出t的值;若不存在,请说明理由.
分析 (1)根据圆的方程求出A,B的坐标,利用△AOB的面积为2,即可求圆C的方程;
(2)求出DE,OC的斜率,即可得出结论.
解答 解:(1)由题设知,圆C的方程为(x-t)2+(y-t)2=2t2,
当y=0时,x=0或2t,则A(2t,0);
当x=0时,y=0或2t,则B(0,2t),
∴S△AOB=$\frac{1}{2}$|OA|•|OB|=$\frac{1}{2}$|2t|•|2t|=2,
∵t>0,
∴t=1.
∴圆C的方程为(x-1)2+(y-1)2=2;
(2)∵|OD|=|OE|,∴OC⊥DE,
∵直线DE的斜率k=-2,OC的斜率为1
∴t=2或t=-2.不满足斜率的积为-1,
∴不存在t使得|OD|=|OE|.
点评 本题主要考查直线和圆的方程的综合应用,根据条件确定圆的方程是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.某种产品的广告费用支出x(千元)与销售额y(万元)之间有如下对应数据:
(参考公式:$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\bar x\bar y}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}},\hat a=\bar y-\hat b\bar x$)
(1)根据上表数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程;
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
(2)当广告费用支出10千元时,预测一下该商品的销售额为多少万元?
| x | 2 | 4 | 5 | 6 | 8 |
| y | 3 | 4 | 6 | 5 | 7 |
(1)根据上表数据,用最小二乘法求出销售额y关于费用支出x的线性回归方程;
(参考值:2×3+4×4+5×6+6×5+8×7=138,22+42+52+62+82=145)
(2)当广告费用支出10千元时,预测一下该商品的销售额为多少万元?
4.在平行四边形ABCD中,对角线AC与BD交于点O,$\overrightarrow{CO}=λ({\overrightarrow{AB}+\overrightarrow{AD}})$,则实数λ=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
1.有分别写着数字1到120的120张卡片,从中取出1张,这样卡片上的数字是2的倍数或是3的倍数的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{7}$ | D. | $\frac{2}{3}$ |
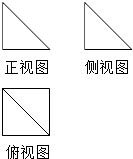 一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.
一个几何体的三视如图所示,其中正视图和俯视图均为腰长为2的等腰直角三角形,则用3个这样的几何体可以拼成一个棱长为2的正方体.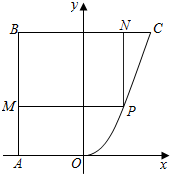 某地有如图所示的一块不规则的非农业用地ABCO,且AB⊥BC,OA∥BC,AB=BC=4km,AO=2km,曲线段OC是以O为顶点,开口向上,且对称轴平行于AB的抛物线的一段.当地政府为科技兴市,欲将该地规划建成一个矩形高科技工业园区PMBN,矩形的相邻两边BM,BN分别落在AB,BC上,顶点P在曲线段OC上.问应如何规划才能使矩形园区的用地面积最大?并求出最大的用地面积(精确到0.1 km2).
某地有如图所示的一块不规则的非农业用地ABCO,且AB⊥BC,OA∥BC,AB=BC=4km,AO=2km,曲线段OC是以O为顶点,开口向上,且对称轴平行于AB的抛物线的一段.当地政府为科技兴市,欲将该地规划建成一个矩形高科技工业园区PMBN,矩形的相邻两边BM,BN分别落在AB,BC上,顶点P在曲线段OC上.问应如何规划才能使矩形园区的用地面积最大?并求出最大的用地面积(精确到0.1 km2).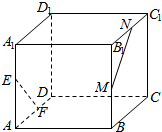 已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.
已知点E,F,M,N分别为正方体ABCD-A1B1C1D1的棱AA1,AD,BB1,B1C1的中点,则异面直线EF和MN所成的角为90°.