题目内容
已知实数x满足2x2≤3x,则函数f(x)=(k2+1)x2-2(k2+1)x+3(k∈R)的最大值 .
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:求出x的取值范围,结合一元二次函数的图象和性质即可得到结论.
解答:
解:由2x2≤3x解得0≤x≤
,
函数f(x)的对称轴为x=-
=1,
∵0≤x≤
,
∴0到对称轴的距离远,
即当x=0时,函数f(x)取得最大值为f(0)=3,
故答案为:3
| 3 |
| 2 |
函数f(x)的对称轴为x=-
| -2(k2+1) |
| 2(k2+1) |
∵0≤x≤
| 3 |
| 2 |
∴0到对称轴的距离远,
即当x=0时,函数f(x)取得最大值为f(0)=3,
故答案为:3
点评:本题主要考查函数最值的求解,根据一元二次函数的性质求出对称轴是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
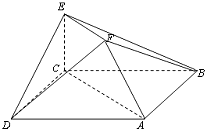 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=| 2 |
(1)求证:平面BEF⊥平面DEF;
(2)求二面角A-BF-E的余弦值.
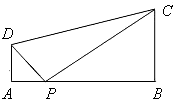 如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.
如图,梯形ABCD中,AD∥BC,AD⊥AB,AD=1,BC=2,AB=3,P是AB上的一个动点,∠DPA=α,∠CPB=β.