题目内容
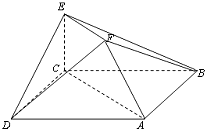 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=| 2 |
(1)求证:平面BEF⊥平面DEF;
(2)求二面角A-BF-E的余弦值.
考点:用空间向量求平面间的夹角,平面与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)连接BD交AC于点O,连接FO,由已知得∠BFD是二面角B-EF-D的平面角,由此能证明平面BEF⊥平面DEF.
(2)取BF中点M,BE中点N,连接AM、MN、AN,由已知得∠AMN就是二面角A-BF-E的平面角,由此能求出二面角A-BF-E的余弦值.
(2)取BF中点M,BE中点N,连接AM、MN、AN,由已知得∠AMN就是二面角A-BF-E的平面角,由此能求出二面角A-BF-E的余弦值.
解答:
(1)证明:∵平面ACEF⊥平面ABCD,EC⊥AC,∴EC⊥平面ABCD.
连接BD交AC于点O,连接FO.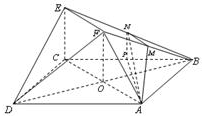
∵正方形ABCD的边长为
,∴AC=BD=2.
在直角梯形ACEF中,∵EF=EC=1,O为AC中点,
∴FO∥EC,且FO=1,
DF=BF=
,DE=BE=
.
由勾股定理知 DF⊥EF,BF⊥EF,
∴∠BFD是二面角B-EF-D的平面角.
由BF=DF=
,BD=2可知∠BFD=90°,
∴平面BEF⊥平面DEF.
(2)解:取BF中点M,BE中点N,连接AM、MN、AN,
∵AB=BF=AF=
,∴AM⊥BF.
又∵MN∥EF,EF⊥BF,∴MN⊥BF,
∴∠AMN就是二面角A-BF-E的平面角.
由题意得AM=
AB=
,MN=
EF=
.
取BC中点P,连接NP,则NP∥EC,
∴NP⊥平面ABCD,连接AP,在Rt△APN中,解得AN2=AP2+NP2=
,
∴在△AMN中,由余弦定理求得cos∠AMN=-
,
即二面角A-BF-E的余弦值为-
.
连接BD交AC于点O,连接FO.

∵正方形ABCD的边长为
| 2 |
在直角梯形ACEF中,∵EF=EC=1,O为AC中点,
∴FO∥EC,且FO=1,
DF=BF=
| 2 |
| 3 |
由勾股定理知 DF⊥EF,BF⊥EF,
∴∠BFD是二面角B-EF-D的平面角.
由BF=DF=
| 2 |
∴平面BEF⊥平面DEF.
(2)解:取BF中点M,BE中点N,连接AM、MN、AN,
∵AB=BF=AF=
| 2 |
又∵MN∥EF,EF⊥BF,∴MN⊥BF,
∴∠AMN就是二面角A-BF-E的平面角.
由题意得AM=
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
取BC中点P,连接NP,则NP∥EC,
∴NP⊥平面ABCD,连接AP,在Rt△APN中,解得AN2=AP2+NP2=
| 11 |
| 4 |
∴在△AMN中,由余弦定理求得cos∠AMN=-
| ||
| 3 |
即二面角A-BF-E的余弦值为-
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
全集U=R,A=N,B={x|-1≤x≤2},则A∩B=( )
| A、{-1,0,1,2} |
| B、{0,1,2} |
| C、[0,2] |
| D、[-1,2] |
定义运算
=ad-bc,若函数f(x)=
在[-4,m]上单调递减,则实数m的取值范围( )
|
|
|
|
| A、[-2,+∞) |
| B、(-∞,-2] |
| C、[-4,-2] |
| D、(-4,-2] |