题目内容
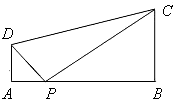如图，梯形ABCD中，AD∥BC，AD⊥AB，AD=1，BC=2，AB=3，P是AB上的一个动点，∠DPA=α，∠CPB=β． （1）求
| PD |
| PC |
（2）求y=tan∠DPC取得最大值时
| PD |
| PC |
考点：平面向量的综合题
专题：计算题,平面向量及应用
分析：（I）以A为原点，AB所在直线为x轴，分别写出点A，B，C，D，P的坐标，利用数量积和二次函数的单调性，即可得出；
（II）利用两角和的正切公式，结合基本不等式即可得出．
（II）利用两角和的正切公式，结合基本不等式即可得出．
解答：
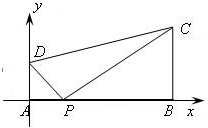解：（1）以A为原点，AB所在直线为x轴，建立如图所示的直角坐标系．
则A（0，0），B（3，0），C（3，2），D（0，1），
令P（x，0），0≤x≤3
有
=（-x，1），
=（3-x，2）
所以
•
=x2-3x+2=（x-1.5）2-0.25，…（3分）
当x=1.5时，
•
最小
此时P（1.5，0）为线段AB中点…（6分）
（2）由（1）知，
•
=x2-3x+2，tanα=
，tanβ=
…（8分）
∵∠DPC=π-β-α，
∴tan∠DPC=-tan（α+β）=
=
≤
=-（4
+9）（0≤x≤3），
当且仅当x+3=2
，即x=2
-3时取到等号，…（10分）
此时
•
=x2-3x+2=40-18
…（12分）
解：（1）以A为原点，AB所在直线为x轴，建立如图所示的直角坐标系．则A（0，0），B（3，0），C（3，2），D（0，1），
令P（x，0），0≤x≤3
有
| PD |
| PC |
所以
| PD |
| PC |
当x=1.5时，
| PD |
| PC |
此时P（1.5，0）为线段AB中点…（6分）
（2）由（1）知，
| PD |
| PC |
| 1 |
| x |
| 2 |
| 3-x |
∵∠DPC=π-β-α，
∴tan∠DPC=-tan（α+β）=
| x+3 |
| x2-3x+2 |
| 1 | ||
x+3+
|
| 1 | ||
4
|
| 5 |
当且仅当x+3=2
| 5 |
| 5 |
此时
| PD |
| PC |
| 5 |
点评：熟练掌握数量积和二次函数的单调性、两角和的正切公式、基本不等式是解题的关键．
练习册系列答案
相关题目