题目内容
已知f（x）是定义于R上的奇函数，当x≥0时，f（x）=|x-a|-a（a＞0），且对任意x∈R，恒有f（x+1）≥f（x），则实数a的取值范围是（ ）
| A、（0，4] | ||
| B、（0，2] | ||
C、（0，
| ||
D、（0，
|
考点：抽象函数及其应用
专题：函数的性质及应用
分析：定义域为R的函数f（x）是奇函数，当x≥0时，f（x）=|x-a|-a，画出函数图象，可得1≥3a-（-a）可得a的范围．
解答：
解：∵f（x）=|x-a|-a=
f（x）的图象如图所示：
当x＜0时，函数的最大值为a，
∵对x∈R，恒有f（x+1）≥f（x），
要满足f（x+l）≥f（x），1大于等于区间长度3a-（-a），
∴1≥3a-（-a）＞0
解得0＜a≤
，
故选：D
|
f（x）的图象如图所示：
当x＜0时，函数的最大值为a，
∵对x∈R，恒有f（x+1）≥f（x），
要满足f（x+l）≥f（x），1大于等于区间长度3a-（-a），
∴1≥3a-（-a）＞0
解得0＜a≤
| 1 |
| 4 |
故选：D
点评：考查学生的阅读能力，应用知识分析解决问题的能力，考查数形结合的能力，用图解决问题的能力，属中档题．
练习册系列答案
相关题目
在极坐标系中，圆C过极点，且圆心的极坐标是（a，
）（a＞0），则圆C的极坐标方程是（ ）
| π |
| 2 |
| A、ρ=-2asinθ |
| B、ρ=2asinθ |
| C、ρ=-2acosθ |
| D、ρ=2acosθ |
下列命题中，正确的是（ ）
| A、若三条直线两两平行，则这三条直线必共面 |
| B、互不平行的两条直线是异面直线 |
| C、分别位于两个不同平面内的两条直线是异面直线 |
| D、不同在任何一个平面内的两条直线是异面直线 |
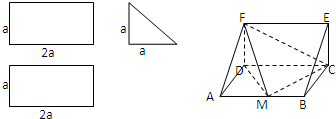一个多面体的三视图和直观图如图所示，其中正视图和俯视图均为矩形，侧视图为直角三角形，M是AB的中点．