题目内容
已知正方体ABCD-A1B1C1D1中，点P在线段A1B1上，点Q在线段B1C1上，且B1P=B1Q，给出下列结论：
①A、C、P、Q四点共面；
②直线PQ与 AB1所成的角为60°；
③PQ⊥CD1；
④VP-ABCD=VQ-AA1D．
其中正确结论的个数是（ ）
①A、C、P、Q四点共面；
②直线PQ与 AB1所成的角为60°；
③PQ⊥CD1；
④VP-ABCD=VQ-AA1D．
其中正确结论的个数是（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：如图所示，①由B1P=B1Q，可得PQ∥A1C1，可得A、C、P、Q四点共面；
②连接AC，CB1，可得△ACB1是等边三角形，可得异面直线PQ与 AB1所成的角为60°；
③由②PQ⊥CD1不正确；
④VP-ABCD=
V正方体AC1，VQ-AA1D=
×S△AA1D×A1B1=
×
S正方形AA1DD1×A1B1=
V正方体，即可判断出．
②连接AC，CB1，可得△ACB1是等边三角形，可得异面直线PQ与 AB1所成的角为60°；
③由②PQ⊥CD1不正确；
④VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
解答：
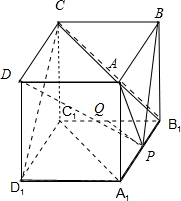解：如图所示，
①∵B1P=B1Q，∴PQ∥A1C1，∴A、C、P、Q四点共面，因此正确；
②连接AC，CB1，可得△ACB1是等边三角形，又AC∥A1C1，∴直线PQ与 AB1所成的角为60°；
③由②PQ⊥CD1不正确；
④VP-ABCD=
V正方体AC1，VQ-AA1D=
×S△AA1D×A1B1=
×
S正方形AA1DD1×A1B1=
V正方体．
∴VP-ABCD≠VQ-AA1D．
其中正确结论的个数2．
故选：B．
解：如图所示，①∵B1P=B1Q，∴PQ∥A1C1，∴A、C、P、Q四点共面，因此正确；
②连接AC，CB1，可得△ACB1是等边三角形，又AC∥A1C1，∴直线PQ与 AB1所成的角为60°；
③由②PQ⊥CD1不正确；
④VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴VP-ABCD≠VQ-AA1D．
其中正确结论的个数2．
故选：B．
点评：本题综合考查了正方体的有关性质，考查了推理能力和计算能力，属于中档题．
练习册系列答案
相关题目
已知R上的连续函数g（x）满足：
①当x＞0时，g′（x）＞0恒成立（g′（x）为函数g（x）的导函数）；
②对任意的x∈R都有g（x）=g（-x），又函数f（x）满足：对任意的x∈R，都有f(
+x)=f(x-
)成立．当x∈[-
，
]时，f（x）=x3-3x．若关于x的不等式g[f（x）]≤g（a2-a+2）对x∈[-
-2
，
+2
]恒成立，则a的取值范围是（ ）
①当x＞0时，g′（x）＞0恒成立（g′（x）为函数g（x）的导函数）；
②对任意的x∈R都有g（x）=g（-x），又函数f（x）满足：对任意的x∈R，都有f(
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| A、a∈R | ||||||||||||
| B、0≤a≤1 | ||||||||||||
C、-
| ||||||||||||
| D、a≤0或a≥1 |
如图，正六边形ABCDEF中，
+
+
=（ ）
| BA |
| CD |
| EF |
A、
| ||
B、
| ||
C、
| ||
D、
|
定义
=a1a4-a2a3，若f（x）=
，则f（x）的图象向右平移
个单位得到的函数解析式为（ ）
|
|
| π |
| 3 |
A、y=2sin（x-
| ||
B、y=2sin（x+
| ||
| C、y=2cosx | ||
| D、y=2sinx |
已知f（x）是定义于R上的奇函数，当x≥0时，f（x）=|x-a|-a（a＞0），且对任意x∈R，恒有f（x+1）≥f（x），则实数a的取值范围是（ ）
| A、（0，4] | ||
| B、（0，2] | ||
C、（0，
| ||
D、（0，
|