题目内容
若直线y=
x+2绕其与y轴的交点逆时针旋转
,则此时直线在x轴上的截距是( )
| 2 |
| 3 |
| π |
| 4 |
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
考点:两直线的夹角与到角问题,直线的截距式方程
专题:直线与圆
分析:设直线y=
x+2的倾斜角为θ,则tanθ=
,根据条直线到另一条直线的角的计算公式求得所得直线的斜率tan(θ+
)的值,用斜截式求出所得直线的方程,可得所得直线在x轴上的截距.
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 4 |
解答:
解:设直线y=
x+2的倾斜角为θ,则tanθ=
,将其绕其与y轴的交点M(0,2)逆时针旋转
,
所得直线的斜率为tan(θ+
)=
=
=5,故所得直线的方程为y=5x+2,
令y=0,求得x=-
,故所得直线在x轴上的截距是-
,
故选:C.
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 4 |
所得直线的斜率为tan(θ+
| π |
| 4 |
| tanθ+1 | ||
1-tanθtan
|
| ||
1-
|
令y=0,求得x=-
| 2 |
| 5 |
| 2 |
| 5 |
故选:C.
点评:本题主要考查直线的倾斜角和斜率的关系,一条直线到另一条直线的角的计算公式,两角和的正切公式,用斜截式求直线的方程,属于基础题.

练习册系列答案
相关题目
如图,在正方体ABCD-A1B1C1D1中,异面直线AD1与BA1所成的角为( )
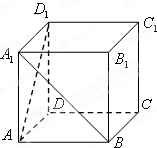

| A、30° | B、45° |
| C、60° | D、90° |
已知数列{an}中,a1=1,且
=
+3(n∈N*),则a2015=( )
| 1 |
| an+1 |
| 1 |
| an |
| A、6042 | ||
| B、6048 | ||
C、
| ||
D、
|
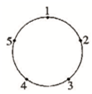 如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按顺时针方向绕圆从一个点跳到另一点;若停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次可以跳两个点,该青蛙从5这点跳起,跳2008次后它将停在的点是( )
如图,圆周上按顺时针方向标有1,2,3,4,5五个点,一只青蛙按顺时针方向绕圆从一个点跳到另一点;若停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次可以跳两个点,该青蛙从5这点跳起,跳2008次后它将停在的点是( )| A、1 | B、2 | C、3 | D、4 |
集合P={(x,y)|y=k},Q={(x,y)|y=ax+1,a>0,a≠1},已知P∩Q只有一个子集,那么实数k的取值范围是( )
| A、(-∞,1) |
| B、(-∞,1] |
| C、(1,+∞) |
| D、(-∞,+∞) |
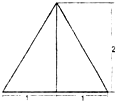 一个三棱锥的侧棱长都相等,底面是正三角形,其正(主)视图如右图所示.该三棱锥侧面积和体积分别是( )
一个三棱锥的侧棱长都相等,底面是正三角形,其正(主)视图如右图所示.该三棱锥侧面积和体积分别是( )A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、8,
|
在△ABC中,根据下列条件解三角形,其中有两个解的是( )
| A、b=10,A=45°,C=60° |
| B、a=6,c=5,B=60° |
| C、a=7,b=5,A=60° |
| D、a=14,b=16,A=45° |
已知f(x)=(ax+2)6,f′(x)是f(x)的导数,若f′(x)的展开式中x的系数大于f(x)的展开式中x的系数,则a的取值范围是( )
A、a>
| ||
B、0<a<
| ||
C、a>
| ||
D、a>
|