题目内容

如图，在正方体ABCD-A1B1C1D1中，异面直线AD1与BA1所成的角为（　　）
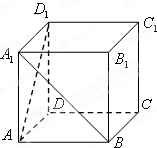
A、30°B、45°
C、60°D、90°
考点：异面直线及其所成的角
专题：空间角
分析：由A1B∥D1C，得异面直线AD1，BA1所成的角为∠AD1C．
解答： 解：∵A1B∥D1C，
∴异面直线AD1，BA1所成的角为∠AD1C，
∵△AD1C为等边三角形，
∴∠AD1C=60°．
故选：C．
点评：本题考查两异面直线所成角的求法，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
设等差数列{an}满足a3=5，a10=-9，Sn是数列{an}的前n项和，则Sn的最大值为
 
．
在长方形ABCD中，AD=1，E为CD的中点，若
AC
•
BE
=-1，则AB的长为
 
．
已知f（x）=x3-3x+m+2，在[0，2]上任取三个数a，b，c，均存在以f（a），f（b），f（c）为边的三角形，则实数m的范围是（　　）
A、m＞2B、m＞4
C、m＞6D、m＞8
规定a?b=
ab
+2a+b，a、b∈R+，若1?k=4，则函数f（x）=k?x的值域（　　）
A、（2，+∞）
B、（1，+∞）
C、[
7
8
，+∞）
D、[
7
4
，+∞）
已知等比数列{an}的首项a1=1，公比q=2，则log2a1+log2a2+…+log2a11=（　　）
A、46B、35C、55D、50
设函数f（x）的定义域为A，且满足任意x∈A恒有 f（x）+f（2-x）=2的函数可以是（　　）
A、f（x）=log2（x+
1+x2
）
B、f（x）=（x-2）3+1
C、f（x）=
x
x-1
D、f（x）=（x-1）2
等比数列{an}的前n项和为Sn，若S3+3S2=0，则公比q=（　　）
A、-2B、2C、3D、-3
若直线y=
2
3
x+2绕其与y轴的交点逆时针旋转
π
4
，则此时直线在x轴上的截距是（　　）
A、-
5
4
B、-
4
5
C、-
2
5
D、
2
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网