题目内容
18.设$α∈(0,\frac{π}{2}),β∈(0,\frac{π}{4})$,且tanα=$\frac{cosβ+sinβ}{cosβ-sinβ}$,则下列正确的是( )| A. | $2α-β=\frac{π}{4}$ | B. | $2α+β=\frac{π}{4}$ | C. | $α-β=\frac{π}{4}$ | D. | $α+β=\frac{π}{4}$ |
分析 根据正切的和与差公式化解可得答案.
解答 解:由tanα=$\frac{cosβ+sinβ}{cosβ-sinβ}$,可得:tanαcosβ-tanαsinβ=cosβ+sinβ,即tanβ=$\frac{tan-1}{1+tanα}$=tan($α-\frac{π}{4}$)
∵$α∈(0,\frac{π}{2}),β∈(0,\frac{π}{4})$,
∴β=$α-\frac{π}{4}$,即$α-β=\frac{π}{4}$,
故选C
点评 本题考查了正切的和与差公式的逆运用.属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列命题正确的是( )
| A. | 若命题p:?x0∈R,x02-x0+1<0,则¬p:?x∉R,x2-x+1≥0 | |
| B. | 命题“若x=y,则cosx=cosy”的逆否命题为真命题 | |
| C. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 | |
| D. | 已知相关变量(x,y)满足线性回归方程:$\stackrel{∧}{y}$=2-3x,若变量x增加一个单位,则y平均增加3个单位 |
3.为了得到函数y=log2$\sqrt{\frac{x+1}{3}}$的图象,可将函数y=log2$\frac{x}{3}$的图象上所有的点的( )
| A. | 纵坐标缩短为原来的$\frac{1}{2}$(横坐标不变),再向左平移1个单位 | |
| B. | 纵坐标缩短为原来的$\frac{1}{2}$(横坐标不变),再向左平移$\frac{1}{3}$个单位 | |
| C. | 横坐标伸长为原来的$\sqrt{2}$倍(纵坐标不变),再向左平移$\frac{1}{3}$个单位 | |
| D. | 横坐标伸长为原来的2倍(纵坐标不变),再向右平移1个单位 |
10.设双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为e,则斜率为k的直线与双曲线C的左、右两支都相交的充要条件是( )
| A. | k2-e2>1 | B. | k2-e2<1 | C. | e2-k2>1 | D. | e2-k2<1 |
7.抛掷一枚质地均匀的骰子两次,记A={两次的点数均为偶数},B={两次的点数之和为8},则P(B|A)=( )
| A. | $\frac{1}{12}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
5.一条直线和直线外三个点最多能确定的平面个数是( )
| A. | 4 | B. | 6 | C. | 7 | D. | 10 |
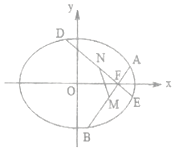 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的离心率$e=\frac{{\sqrt{2}}}{2}$,且过点$(\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2})$.