题目内容
关于x的方程sinx+
cosx=a（0≤x≤
）有两相异根，则实数a的取值范围是 ．
| 3 |
| π |
| 2 |
考点：两角和与差的正弦函数,函数的零点
专题：常规题型,三角函数的图像与性质
分析：利用两角和的正弦公式化成2sin（x+
）=a，转化研究函数y=2sin（x+
）的图象与函数y=a的图象有两个交点．
| π |
| 3 |
| π |
| 3 |
解答：
解：∵sinx+
cosx=2sin（x+
）
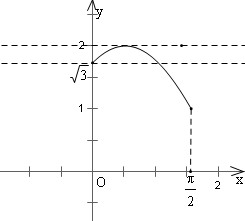
画出y=2sin（x+
）的图象
画出y=a的图象
当
≤a＜2是两图象有两个不同的交点
所以方程sinx+
cosx=a（0≤x≤
）有两相异根时，实数a的取值范围是[
，2）．
故答案为：[
，2）．
| 3 |
| π |
| 3 |
画出y=2sin（x+
| π |
| 3 |
画出y=a的图象
当
| 3 |
所以方程sinx+
| 3 |
| π |
| 2 |
| 3 |
故答案为：[
| 3 |
点评：本题考查了两角和的正弦公式及方程的解的个数问题，解决本题的关键是把方程解的个数问题转化成两函数图象的交点个数问题解决．
练习册系列答案
阅读快车系列答案
相关题目
函数y=（cosx+sinx）•（cosx-sinx）的最小正周期是（ ）
A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |