题目内容
“ab＜0”是“方程ax2+by2=c（a、b、c∈R）表示双曲线”的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分又不必要 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：结合双曲线的定义和方程，利用充分条件和必要条件的定义进行判断．
解答：
解：若方程ax2+by2=c表示双曲线，
则方程等价为
+
=1，即
＜0，
∴ab＜0且c≠0，
∴“ab＜0”是“方程ax2+by2=c（a、b、c∈R）表示双曲线”的必要不充分条件，
故选：B．
则方程等价为
| x2 | ||
|
| y2 | ||
|
| c2 |
| ab |
∴ab＜0且c≠0，
∴“ab＜0”是“方程ax2+by2=c（a、b、c∈R）表示双曲线”的必要不充分条件，
故选：B．
点评：本题主要考查充分条件和必要条件的判断，利用双曲线的定义和方程求出ab＜0是解决本题的关键，比较基础．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
由点P（4，3）引圆x2+y2=9的切线，则切线的长为（ ）
| A、5 | B、4 | C、3 | D、2 |
若某空间几何体的三视图如图所示，则该几何体的表面积是（ ）
| A、60 | B、54 | C、48 | D、24 |
设f（x）=xex，若f′（xo）=0，则x0等于（ ）
| A、e2 | ||
| B、-1 | ||
C、
| ||
| D、ln2 |
若f（x）=x2+（2tanθ）x-1在[-1 ，
]上为减函数，则θ的取值范围是（ ）
| 3 |
A、（-
| ||||
B、[
| ||||
C、（-
| ||||
D、[
|
设函数f（x）可导，则
等于（ ）
| lim |
| △x→0 |
| f(15+3△x)-f(15) |
| △x |
| A、f′（15） | ||
| B、3f′（15） | ||
C、
| ||
| D、f′（3） |
已知函数y=f（2x）+x是偶函数，且f（2）=1，则f（-2）=（ ）
| A、2 | B、3 | C、4 | D、5 |
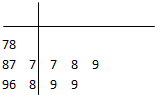学校为测评班级学生对任课教师的满意度，采用“100分制”打分的方式来计分．现从某班学生中随机抽取10名，以下茎叶图记录了他们对某教师的满意度分数（以十位数字为茎，个位数字为叶）：