题目内容
设函数f（x）可导，则
等于（ ）
| lim |
| △x→0 |
| f(15+3△x)-f(15) |
| △x |
| A、f′（15） | ||
| B、3f′（15） | ||
C、
| ||
| D、f′（3） |
考点：定积分
专题：导数的概念及应用
分析：根据导数的定义，即可得到结论
解答：
解：
=3
=3f′（15），
故选：B．
| lim |
| △x→0 |
| f(15+3△x)-f(15) |
| △x |
| lim |
| △x→0 |
| f(3△x+15)-f(15) |
| 3△x |
故选：B．
点评：本题主要考查导数的概念，利用导数的定义是解决本题的关键，比较基础．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
“x＜-1”是“x＜0”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“ab＜0”是“方程ax2+by2=c（a、b、c∈R）表示双曲线”的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分又不必要 |
函数f（x）=log2（x+1）+
的定义域为（ ）
| 4-x2 |
| A、（-1，2] |
| B、（-1，2） |
| C、[-1，2） |
| D、[-1，2] |
如图是一个几何体的三视图，则这个几何体是（ ）
| A、圆柱 | B、圆台 | C、圆锥 | D、棱台 |
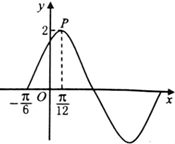已知函数f（x）=Asin（ωx+φ），（ω＞0，A＞0，φ∈（0，