题目内容
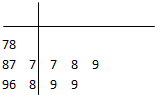 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):(Ⅰ)指出这组数据的众数和中位数;
(Ⅱ)若满意度不低于98分,则评价该教师为“优秀”.求从这10人中随机选取3人,至多有1人评价该教师是“优秀”的概率;
(Ⅲ)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记ξ表示抽到评价该教师为“优秀”的人数,求ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,众数、中位数、平均数,互斥事件的概率加法公式
专题:应用题,概率与统计
分析:(Ⅰ)根据所给的茎叶图以及众数和中位数的概念,得出众数与中位数;
(Ⅱ)设Ai表示所取3人中有i个人评价该教师为“优秀”,至多有1人评价该教师为“优秀”记为事件A,则P(A)=P(A0)+P(A1),可得答案.
(Ⅲ)ξ可以取0,1,2,3,利用独立事件概率公式,可求出ξ的分布列,代入数学期望公式,可得答案.
(Ⅱ)设Ai表示所取3人中有i个人评价该教师为“优秀”,至多有1人评价该教师为“优秀”记为事件A,则P(A)=P(A0)+P(A1),可得答案.
(Ⅲ)ξ可以取0,1,2,3,利用独立事件概率公式,可求出ξ的分布列,代入数学期望公式,可得答案.
解答:
解:(Ⅰ)根据茎叶图知,这组数据的众数:87;中位数:88.5 …(2分)
(Ⅱ)设Ai表示所取3人中有i个人评价该教师为“优秀”,至多有1人评价该教师为“优秀”记为事件A,则P(A)=P(A0)+P(A1)=
+
=
…(6分)
(Ⅲ)ξ的可能取值为0、1、2、3 …(7分)
P(ξ=0)=(
)3=
;P(ξ=1)=
•
•(
)2=
P(ξ=2)=
•(
)2•
=
;P(ξ=3)=(
)3=
分布列为
…(11分)
Eξ=0×
+1×
+2×
+3×
=0.9.…(12分)
(Ⅱ)设Ai表示所取3人中有i个人评价该教师为“优秀”,至多有1人评价该教师为“优秀”记为事件A,则P(A)=P(A0)+P(A1)=
| ||
|
| ||||
|
| 49 |
| 60 |
(Ⅲ)ξ的可能取值为0、1、2、3 …(7分)
P(ξ=0)=(
| 7 |
| 10 |
| 342 |
| 1000 |
| C | 1 3 |
| 3 |
| 10 |
| 7 |
| 10 |
| 441 |
| 1000 |
P(ξ=2)=
| C | 2 3 |
| 3 |
| 10 |
| 7 |
| 10 |
| 189 |
| 1000 |
| 3 |
| 10 |
| 27 |
| 1000 |
分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
Eξ=0×
| 342 |
| 1000 |
| 441 |
| 1000 |
| 189 |
| 1000 |
| 27 |
| 1000 |
点评:本题考查的知识点是离散型随机变量的期望,茎叶图,古典概型,是概率与统计的综合应用,难度中档.

练习册系列答案
相关题目
“ab<0”是“方程ax2+by2=c(a、b、c∈R)表示双曲线”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分又不必要 |
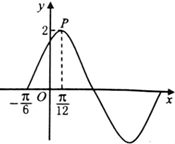 已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,
已知函数f(x)=Asin(ωx+φ),(ω>0,A>0,φ∈(0,