题目内容
在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),若AB=2,BC=
.
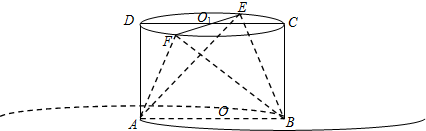
(Ⅰ)设平面BEF与⊙O所在平面的交线为l,平面ABE与⊙O1所在平面的交线为m,证明:l⊥m;
(Ⅱ)将△AEC绕直线AD旋转一周,求所得几何体的体积.
| 2 |

(Ⅰ)设平面BEF与⊙O所在平面的交线为l,平面ABE与⊙O1所在平面的交线为m,证明:l⊥m;
(Ⅱ)将△AEC绕直线AD旋转一周,求所得几何体的体积.
考点:旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)由于圆柱的两底面互相平行,结合面面平行的性质定理可得l∥EF,m∥AB,进而由EF⊥CD得到结论;
(II)依题意,所的几何体是一个大圆锥挖去一个小圆锥,分别求出两个圆锥的体积,相减可得答案.
(II)依题意,所的几何体是一个大圆锥挖去一个小圆锥,分别求出两个圆锥的体积,相减可得答案.
解答:
证明:(Ⅰ)由于圆柱的两底面互相平行,AB?⊙O所在平面
∴AB∥⊙O1所在平面,
同理EF∥⊙O所在平面.…(2分)
又平面BEF与⊙O所在平面的交线为l,
∴l∥EF,
同理由平面ABE与⊙O1所在平面的交线为m可得:m∥AB.…(4分)
又∵EF⊥CD.
故l⊥m.…(6分)
(Ⅱ)依题意,所的几何体是一个大圆锥挖去一个小圆锥,…(8分)
∵AB=2,BC=
.
∴两个圆锥的底面半径分别为DE=
,DC=2,
高均为AD=
.…(10分)
所以其体积V=
π(4-2)×
=
π.…(12分)
∴AB∥⊙O1所在平面,
同理EF∥⊙O所在平面.…(2分)
又平面BEF与⊙O所在平面的交线为l,
∴l∥EF,
同理由平面ABE与⊙O1所在平面的交线为m可得:m∥AB.…(4分)
又∵EF⊥CD.
故l⊥m.…(6分)
(Ⅱ)依题意,所的几何体是一个大圆锥挖去一个小圆锥,…(8分)
∵AB=2,BC=
| 2 |
∴两个圆锥的底面半径分别为DE=
| 2 |
高均为AD=
| 2 |
所以其体积V=
| 1 |
| 3 |
| 2 |
2
| ||
| 3 |
点评:本题考查的知识点是旋转体,圆锥的体积公式,空间直线垂直,是立体几何知识的简单综合应用.

练习册系列答案
相关题目
“a=2”是“直线2x+ay-1=0与直线ax+3y-2=0平行”的( )
| A、充分必要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
 如图,在△ABC中,BC=2,BC边上的高AD=1,P是BC边上任一点,PE∥AB交AC于点E,PF∥AC交AB于点F.
如图,在△ABC中,BC=2,BC边上的高AD=1,P是BC边上任一点,PE∥AB交AC于点E,PF∥AC交AB于点F.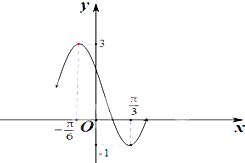 已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<
已知函数g(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<