题目内容
已知f(x)=x-k2+k+2(k∈z)满足f(2)<f(3).
①求k及f(x);
②判断是否存在q>0使g(x)=1-qf(x)+(2q-1)x在[-1,2]上的值域为[-4,
],若存在求出q;若不存在,说明理由.
①求k及f(x);
②判断是否存在q>0使g(x)=1-qf(x)+(2q-1)x在[-1,2]上的值域为[-4,
| 17 |
| 8 |
考点:幂函数的单调性、奇偶性及其应用,幂函数图象及其与指数的关系,幂函数的性质
专题:函数的性质及应用
分析:①根据幂函数的性质即可求k及f(x);
②结合二次函数的定义域和值域之间的关系建立条件关系即可得到结论.
②结合二次函数的定义域和值域之间的关系建立条件关系即可得到结论.
解答:
解:①∵f(2)<f(3).
∴函数f(x)在(0,+∞)上为增函数,
则-k2+k+2>0,
即k2-k-2<0,
解得-1<k<2,
∵k∈z,∴k=0,或1,
当k=0时,f(x)=x2,
当k=1时,f(x)=x2;
②∵f(x)=x2,
∴g(x)=-qx2+(2q-1)x+1,
∵q>0,∴g(-1)=2-3q<2,g(2)=-1,
若存在q>0使g(x)=1-qf(x)+(2q-1)x在[-1,2]上的值域为[-4,
],
则必有g(-1)=2-3q=-4,解得q=2,
此时g(x)=-2x2+3x+1=-2(x-
)2+
,
∵x∈[-1,2],
∴当x=
时,函数取得最大值
,
当x=-1时,函数取得最小值-4,此时满足函数的值域为[-4,
],
故存在q=2,使条件成立.
∴函数f(x)在(0,+∞)上为增函数,
则-k2+k+2>0,
即k2-k-2<0,
解得-1<k<2,
∵k∈z,∴k=0,或1,
当k=0时,f(x)=x2,
当k=1时,f(x)=x2;
②∵f(x)=x2,
∴g(x)=-qx2+(2q-1)x+1,
∵q>0,∴g(-1)=2-3q<2,g(2)=-1,
若存在q>0使g(x)=1-qf(x)+(2q-1)x在[-1,2]上的值域为[-4,
| 17 |
| 8 |
则必有g(-1)=2-3q=-4,解得q=2,
此时g(x)=-2x2+3x+1=-2(x-
| 3 |
| 4 |
| 17 |
| 8 |
∵x∈[-1,2],
∴当x=
| 3 |
| 4 |
| 17 |
| 8 |
当x=-1时,函数取得最小值-4,此时满足函数的值域为[-4,
| 17 |
| 8 |
故存在q=2,使条件成立.
点评:本题主要考查了幂函数的单调性,以及二次函数的值域,同时考查了分析问题的能力.

练习册系列答案
相关题目
如图,平面正六边形ABCDEF中,不能和
组成平面向量基底的是( )

| AB |

A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
用更相减损术求30和18的最大公约数时,第三次作的减法为( )
| A、18-16=6 |
| B、12-6=6 |
| C、6-6=0 |
| D、30-18=12 |
在等差数列{an}中,若a3=2,a5=8,则S7等于( )
| A、16 | B、18 | C、35 | D、22 |
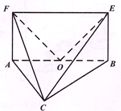 如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.
如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC,O为AB的中点,OF⊥EC.