题目内容
6．
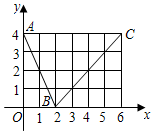如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f′（1）+f（3）=（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 方法一：根据图象求出函数的解析式，再根据导数运算法则，即可求出导数值和函数值，问题得以解决，
方法二：根据导数的几何意义可得，f′（1）等于直线AB的斜率，根据图象可得f（3）=1，问题得以解决．
解答 解：方法一：∵A，B，C的坐标分别为（0，4），（2，0），（6，4），
∴直线AB的方程为y=-2x+4，直线BC的方程为y=x-2，
∴f（x）=$\left\{\begin{array}{l}{-2x+4，x≤2}\\{x-2，x＞2}\end{array}\right.$，
当x≤2时，f′（x）=-2，
∴f′（1）+f（3）=-2+3-2=-1，
方法二：f′（1）=KAB=$\frac{4-0}{0-2}$=-2，根据图象可得f（3）=1，
∴f′（1）+f（3）=-2+3-2=-1，
故选：A．
点评 本题考查了直线的斜率公式和导数的几何意义，属于基础题．
练习册系列答案
相关题目
14．已知函数$f（x）={sin^4}x+{cos^4}x，x∈[-\frac{π}{4}，\frac{π}{4}]$，若f（x1）＜f（x2），则一定有（ ）
| A． | x1＜x2 | B． | x1＞x2 | C． | ${x_1}^2＜{x_2}^2$ | D． | ${x_1}^2＞{x_2}^2$ |
12．若实数x，y满足$\left\{\begin{array}{l}{x-2y+3≥0}\\{y≥x}\\{x≥1}\end{array}\right.$，则z=$\sqrt{{x}^{2}+{y}^{2}}$的最小值为（ ）
| A． | 3 | B． | $\sqrt{5}$ | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
9．已知正数a，b满足a+b=4，则曲线f（x）=lnx+$\frac{x}{b}$在点（a，f（a））处的切线的倾斜角的取值范围为（ ）
| A． | [$\frac{π}{4}$，+∞） | B． | [$\frac{π}{4}$，$\frac{5π}{12}$） | C． | [$\frac{π}{4}$，$\frac{π}{2}$） | D． | [$\frac{π}{4}$，$\frac{π}{3}$） |
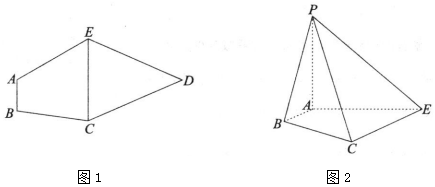
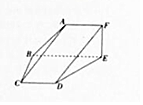如图，平面ABEF⊥平面CBED，四边形ABEF为直角三角形，∠AFE=∠FEB=90°，四边形CBED为等腰梯形，CD∥BE，且BE=2AF=2CD=2BC=2EF=4．