题目内容
14.已知函数$f(x)={sin^4}x+{cos^4}x,x∈[-\frac{π}{4},\frac{π}{4}]$,若f(x1)<f(x2),则一定有( )| A. | x1<x2 | B. | x1>x2 | C. | ${x_1}^2<{x_2}^2$ | D. | ${x_1}^2>{x_2}^2$ |
分析 把已知函数解析式变形,由f(x1)<f(x2),得sin22x1>sin22x2,即|sin2x1|>|sin2x2|,再由x1,x2的范围可得|2x1|>|2x2|,即|x1|>|x2|,得到${{x}_{1}}^{2}>{{x}_{2}}^{2}$.
解答 解:f(x)=sin4x+cos4x=(sin2x+cos2x)2-2sin2xcos2x=$1-\frac{1}{2}si{n}^{2}2x$.
由f(x1)<f(x2),得$1-\frac{1}{2}si{n}^{2}2{x}_{1}<1-\frac{1}{2}si{n}^{2}2{x}_{2}$,
∴sin22x1>sin22x2,即|sin2x1|>|sin2x2|,
∵x1∈[-$\frac{π}{4},\frac{π}{4}$],x2∈[-$\frac{π}{4},\frac{π}{4}$],
∴2x1∈[-$\frac{π}{2}$,$\frac{π}{2}$],2x2∈[-$\frac{π}{2},\frac{π}{2}$],
由|sin2x1|>|sin2x2|,得|2x1|>|2x2|,即|x1|>|x2|,∴${{x}_{1}}^{2}>{{x}_{2}}^{2}$.
故选:D.
点评 本题考查三角函数的化简求值,考查三角函数线的应用,属中档题.

练习册系列答案
相关题目
4.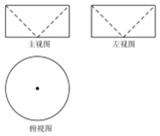 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )
 如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )
如图是一个几何体挖去另一个几何体所得的三视图,若主视图中长方形的长为2,宽为1,则该几何体的体积为( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
2.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x-3,x≤1}\\{lnx,x>1}\end{array}\right.$若|f(x)|+a≥ax,则a的取值范围是( )
| A. | [-2,0) | B. | [0,1] | C. | (0,1] | D. | [-2,0] |
9.已知集合A={x|1<x2<4},B={x|x-1≥0},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (-1,2) | D. | [-1,2) |
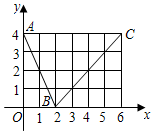 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )