题目内容

17．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（x，-2），若$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直，则实数x的值是（　　）
A．±1B．1C．-1D．-4

分析 利用平面向量坐标运算法则分别求出$\overrightarrow{a}$+$\overrightarrow{b}$，$\overrightarrow{a}$-$\overrightarrow{b}$，再由$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直，能求出实数x的值．

解答 解：∵向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（x，-2），
∴$\overrightarrow{a}$+$\overrightarrow{b}$=（1+x，0），$\overrightarrow{a}$-$\overrightarrow{b}$=（1-x，4），
∵$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直，
∴（$\overrightarrow{a}+\overrightarrow{b}$）（$\overrightarrow{a}-\overrightarrow{b}$）=（1+x）（1-x）+0=0，
解得x=±1．
故选：A．

点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意平面向量坐标运算法则、向量垂直的性质的合理运用．

练习册系列答案
相关题目
7．设函数f（x）=$\left\{\begin{array}{l}{1+cos\frac{πx}{2}，x＞1}\\{x^2，0＜x≤1}\end{array}\right.$，函数g（x）=x+$\frac{1}{x}$+a（x＞0），若存在唯一的x0，使得h（x）=min{f（x），g（x）}的值为h（x0），则实数a的取值范围为（-∞，-2）．
8．设全集U=R，集合A={x|x＞0}，B={x|x2-x-2＜0}，则A∩（∁UB）=（　　）
A．（0，2]B．（-1，2]C．[-1，2]D．[2，+∞）
5．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=3+t}\\{y=1+at}\end{array}\right.$（t为参数，a∈R），曲线C的参数方程为$\left\{\begin{array}{l}{x=2+2cosα}\\{y=2sinα}\end{array}\right.$（α为参数），设直线l与曲线C交于A、B两点，当弦长|AB|最短时，直线l的普通方程为x+y-4=0．
12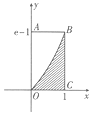．图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成，现向矩形区域OABC内随机投掷一点，则该点落在非阴影区域的概率是（　　）
A．$\frac{1}{e}$B．$\frac{1}{e-1}$C．1-$\frac{1}{e}$D．1-$\frac{1}{e-1}$
2．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+4x-3，x≤1}\\{lnx，x＞1}\end{array}\right.$若|f（x）|+a≥ax，则a的取值范围是（　　）
A．[-2，0）B．[0，1]C．（0，1]D．[-2，0]
9．已知集合A={x|1＜x2＜4}，B={x|x-1≥0}，则A∩B=（　　）
A．（1，2）B．[1，2）C．（-1，2）D．[-1，2）
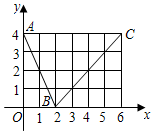6．如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f′（1）+f（3）=（　　）
A．-1B．0C．1D．2
1．设集合A={x|（x+1）（4-x）＞0}，B={x|0＜$\sqrt{x}$＜3}，则A∩B等于（　　）
A．（0，4）B．（4，9）C．（-1，4）D．（-1，9）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网