题目内容
1.如图1,平面五边形ABCDE中,AB∥CE,且$AE=2,∠AEC={60°},CD=ED=\sqrt{7}$,$cos∠EDC=\frac{5}{7}$.将△CDE沿CE折起,使点D到P的位置如图2,且$AP=\sqrt{3}$,得到四棱锥P-ABCE.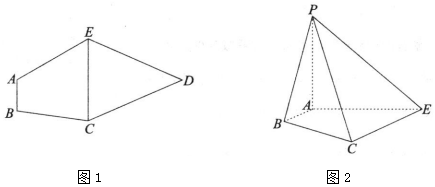
(1)求证:AP⊥平面ABCE;
(2)记平面PAB与平面PCE相交于直线l,求证:AB∥l.
分析 (1)在△CDE中,由已知结合余弦定理得CE.连接AC,可得AC=2.在△PAE中,由PA2+AE2=PE2,得AP⊥AE.同理,AP⊥AC,然后利用线面垂直的判定可得AP⊥平面ABCE;
(2)由AB∥CE,且CE?平面PCE,AB?平面PCE,可得AB∥平面PCE,又平面PAB∩平面PCE=l,结合面面平行的性质可得AB∥l.
解答 证明:(1)在△CDE中,∵$CD=ED=\sqrt{7}$,$cos∠EDC=\frac{5}{7}$,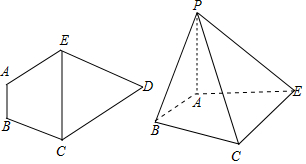
∴由余弦定理得CE=$\sqrt{(\sqrt{7})^{2}+(\sqrt{7})^{2}-2×\sqrt{7}×\sqrt{7}×\frac{5}{7}}$=2.
连接AC,∵AE=2,∠AEC=60°,∴AC=2.
又∵$AP=\sqrt{3}$,∴在△PAE中,PA2+AE2=PE2,
即AP⊥AE.
同理,AP⊥AC,
∵AC?平面ABCE,AE?平面ABCE,
且AC∩AE=A,
故AP⊥平面ABCE;
(2)∵AB∥CE,且CE?平面PCE,AB?平面PCE,
∴AB∥平面PCE,
又平面PAB∩平面PCE=l,
∴AB∥l.
点评 本题考查线面垂直的判定,面面平行的性质,考查空间想象能力和思维能力,关键是明确折叠问题折叠前后的变量与不变量,是中档题.

练习册系列答案
相关题目
12.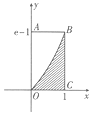 图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )
图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )
 图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )
图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成,现向矩形区域OABC内随机投掷一点,则该点落在非阴影区域的概率是( )| A. | $\frac{1}{e}$ | B. | $\frac{1}{e-1}$ | C. | 1-$\frac{1}{e}$ | D. | 1-$\frac{1}{e-1}$ |
9.已知集合A={x|1<x2<4},B={x|x-1≥0},则A∩B=( )
| A. | (1,2) | B. | [1,2) | C. | (-1,2) | D. | [-1,2) |
16.锐角△ABC中,内角A,B,C的对边分别为a,b,c,且满足(a-b)(sinA+sinB)=(c-b)sinC,若$a=\sqrt{3}$,则b2+c2的取值范围是( )
| A. | (5,6] | B. | (3,5) | C. | (3,6] | D. | [5,6] |
5.设函数f(x)=$\frac{3}{2}{x^2}-2ax({a>0})$与g(x)=a2lnx+b有公共点,且在公共点处的切线方程相同,则实数b的最大值为( )
| A. | $\frac{1}{{2{e^2}}}$ | B. | $\frac{1}{2}{e^2}$ | C. | $\frac{1}{e}$ | D. | $-\frac{3}{{2{e^2}}}$ |
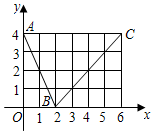 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )