题目内容
9.已知正数a,b满足a+b=4,则曲线f(x)=lnx+$\frac{x}{b}$在点(a,f(a))处的切线的倾斜角的取值范围为( )| A. | [$\frac{π}{4}$,+∞) | B. | [$\frac{π}{4}$,$\frac{5π}{12}$) | C. | [$\frac{π}{4}$,$\frac{π}{2}$) | D. | [$\frac{π}{4}$,$\frac{π}{3}$) |
分析 求导数,确定切线斜率的范围,即可求出切线的倾斜角的取值范围.
解答 解:∵f(x)=lnx+$\frac{x}{b}$,
∴f′(x)=$\frac{1}{x}$+$\frac{1}{b}$,
∴f′(a)=$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{4}$($\frac{1}{a}$+$\frac{1}{b}$)(a+b)=$\frac{1}{4}$(2+$\frac{b}{a}$+$\frac{a}{b}$)≥$\frac{1}{4}$(2+2)=1,
当且仅当a=b=2时取等号,∴曲线f(x)=lnx+$\frac{x}{b}$在点(a,f(a))处的切线的倾斜角的取值范围为[$\frac{π}{4}$,$\frac{π}{2}$),
故选C.
点评 本题考查导数的几何意义,考查切线的倾斜角的取值范围,正确求导是关键.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
14.若a=log1664,b=lg0.2,c=20.2,则( )
| A. | c<b<a | B. | b<a<c | C. | a<b<c | D. | b<c<a |
1.设集合A={x|(x+1)(4-x)>0},B={x|0<$\sqrt{x}$<3},则A∩B等于( )
| A. | (0,4) | B. | (4,9) | C. | (-1,4) | D. | (-1,9) |
18.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-2y≥-2}\\{3x-2y≤3}\end{array}\right.$,则z=x+2y的最大值是7.
19.函数y=$\sqrt{x-1}$的定义域是( )
| A. | (0,+∞) | B. | (1,+∞) | C. | [0,+∞) | D. | [1,+∞) |
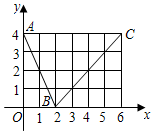 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f′(1)+f(3)=( )