题目内容
8．从抛物线x2=4y上一点P引抛物线准线的垂线，垂足为M，且|PM|=5，设抛物线的焦点为F，则三角形MPF的面积为10．分析 先设处P点坐标，求出抛物线的准线方程，求得P点横坐标，代入抛物线方程求得P的纵坐标，进而利用三角形面积公式求得答案．
解答 解：抛物线x2=4y上一点P引抛物线准线的垂线，
设P（x0，y0）
依题意可知抛物线准线y=-1，
∴y0=5-1=4．
∴|x0|=$\sqrt{4×4}$=4，
∴△MPF的面积为：$\frac{1}{2}\left|PM\right|•\left|{x}_{0}\right|$=$\frac{1}{2}$×5×4=10．
故答案为：10．
点评 本题主要考查了抛物线的应用．抛物线的简单性质，解题的关键是灵活利用了抛物线的定义．
练习册系列答案
习题精选系列答案
相关题目
19．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}x，（x＞0）}\\{{2}^{x}，（x≤0）}\end{array}\right.$则f（f（$\frac{1}{3}$））=（ ）
| A． | -2 | B． | $-\frac{1}{2}$ | C． | 0 | D． | $\frac{1}{2}$ |
16．
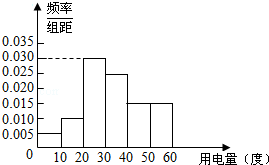某市政府为了确定一个较为合理的居民用电标准，必须先了解全市居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2012年的月均用电量（单位：度）数据，样本统计结果如下图表：
（1）求月均用电量的中位数与平均数估计值；
（2）如果用分层抽样的方法从这n位居民中抽取8位居民，再从这8位居民中选2位居民，那么至少有1位居民月均用电量在30至40度的概率是多少？
（3）用样本估计总体，把频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用电量在30至40度的居民数X的分布列．
某市政府为了确定一个较为合理的居民用电标准，必须先了解全市居民日常用电量的分布情况．现采用抽样调查的方式，获得了n位居民在2012年的月均用电量（单位：度）数据，样本统计结果如下图表：| 分 组 | 频 数 | 频 率 |
| [0，10） | 0.05 | |
| [10，20） | 0.10 | |
| [20，30） | 30 | |
| [30，40） | 0.25 | |
| [40，50） | 0.15 | |
| [50，60] | 15 | |
| 合 计 | n | 1 |
（2）如果用分层抽样的方法从这n位居民中抽取8位居民，再从这8位居民中选2位居民，那么至少有1位居民月均用电量在30至40度的概率是多少？
（3）用样本估计总体，把频率视为概率，从这个城市随机抽取3位居民（看作有放回的抽样），求月均用电量在30至40度的居民数X的分布列．
20．已知平面向量$\overrightarrow a，\overrightarrow b，\overrightarrow c$满足$\overrightarrow c=x\overrightarrow a+y\overrightarrow b$（x，y∈R），且$\overrightarrow a•\overrightarrow c＞0$，$\overrightarrow b•\overrightarrow c＞0$．（ ）
| A． | 若$\overrightarrow a•\overrightarrow b＜0$，则x＞0，y＞0 | B． | 若$\overrightarrow a•\overrightarrow b＜0$，则x＜0，y＜0 | ||
| C． | 若$\overrightarrow a•\overrightarrow b＞0$，则x＜0，y＜0 | D． | 若$\overrightarrow a•\overrightarrow b＞0$，则x＞0，y＞0 |