题目内容
如图，在Rt△ABC中，∠ACB=90°，∠BAC=60°，AC=4，点M在线段AB上．（1）若CM=
| 13 |
（2）若点N在线段MB上，且∠MCN=30°，求△MCN的面积最小值并求△MCN的最小面积时MN的长．
考点：解三角形的实际应用,基本不等式
专题：转化思想,解三角形
分析：（1）CM=
，直接利用余弦定理求AM的长；
（2）设∠ACM=α，α∈[0°，60°]在△ACN中，由正弦定理求出CN，在△ACM中，由正弦定理求出CM，然后表示出△MCN的面积，利用三角函数的有界性求出三角形面积的最小值并求△MCN的最小面积时MN的长．
| 13 |
（2）设∠ACM=α，α∈[0°，60°]在△ACN中，由正弦定理求出CN，在△ACM中，由正弦定理求出CM，然后表示出△MCN的面积，利用三角函数的有界性求出三角形面积的最小值并求△MCN的最小面积时MN的长．
解答：
解：（1）在Rt△ABC中，∠ACB=90°，∠BAC=60°，AC=4，点M在线段AB上．
∵CM=
，
∴CM2=AC2+AM2-2AC•AMcosA；
即13=16+AM2-4•AM，
解得AM=1或AM=3．
（2）设∠ACM=α，α∈[0°，60°]在△ACN中，由正弦定理得：
=
=
=
∴CN=
．
在△ACM中，由正弦定理得：
=
=
∴CM=
．
∴S△MCN=
CM•CNsin∠MCN=
=
，
∵0°≤α≤60°
∴60°≤2α+60°≤180°，
∴0≤sin（2α+60°）≤1
∴当α=15°时，△MCN的面积最小为：24-12
，
此时MN最小值为
=4
-6．
（1）在Rt△ABC中，∠ACB=90°，∠BAC=60°，AC=4，点M在线段AB上．∵CM=
| 13 |
∴CM2=AC2+AM2-2AC•AMcosA；
即13=16+AM2-4•AM，
解得AM=1或AM=3．
（2）设∠ACM=α，α∈[0°，60°]在△ACN中，由正弦定理得：
| CN |
| sinA |
| AC |
| sin∠CNA |
| AC |
| sin(90°+α) |
| AC |
| cosα |
∴CN=
2
| ||
| cosα |
在△ACM中，由正弦定理得：
| CM |
| sinA |
| AC |
| sin∠AMC |
| AC |
| sin(60°+α) |
∴CM=
2
| ||
| sin(60°+α) |
∴S△MCN=
| 1 |
| 2 |
| 3 |
| sin(60°+α)cosα |
| 12 | ||
2sin(2α+60°)+
|
∵0°≤α≤60°
∴60°≤2α+60°≤180°，
∴0≤sin（2α+60°）≤1
∴当α=15°时，△MCN的面积最小为：24-12
| 3 |
此时MN最小值为
24-12
| ||
2
|
| 3 |
点评：本题考查正弦定理与余弦定理的应用，三角函数的以及的应用，考查转化思想以及计算能力．
练习册系列答案
相关题目
某教育机构随机某校20个班级，调查各班关注汉字听写大赛的学生人数，根据所得数据的茎叶图，以组距为5将数据分组成[0，5），[5，10），[10，15），[15，20），[20，25），[25，30），[30，35），[35，40]时，所作的频率分布直方图如图所示，则原始茎叶图可能是（ ）
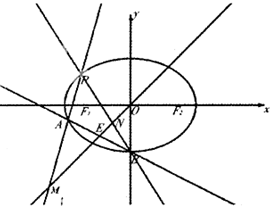已知椭圆C：