题目内容
变量x,y满足约束条件
时,x-2y+m≤0恒成立,则实数m的取值范围为( )
|
| A、[0,+∞) |
| B、[1,+∞) |
| C、(-∞,3] |
| D、(-∞,0] |
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,x-2y+m≤0表示了直线上方的部分,故由
解得,x=4,y=2;代入即可.
|
解答:
解:由题意作出其平面区域,

x-2y+m≤0表示了直线上方的部分,
故由
解得,x=4,y=2;
则4-2×2+m≤0,
则m≤0.
故选D.

x-2y+m≤0表示了直线上方的部分,
故由
|
则4-2×2+m≤0,
则m≤0.
故选D.
点评:本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
相关题目
若f(x)=x2-2(a-1)x+2在(-∞,3]上是减函数,则a的取值范围是( )
| A、a>4 | B、a<4 |
| C、a≥4 | D、a≤4 |
已知函数:f(x)=x2-4|x|+1,若关于x的方程:f(x)=2k恰有四个不等的实数根,则实数k的取值范围为( )
A、-
| ||||
| B、-3<k<1 | ||||
| C、-6<k<2 | ||||
D、k>-
|
已知F是抛物线x2=4y的焦点,P是该抛物线上的动点,则线段PF中点轨迹方程是( )
A、x2=y-
| ||
B、x2=2y-
| ||
| C、x2=2y-2 | ||
| D、x2=2y-1 |
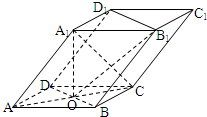 如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=
如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,AB=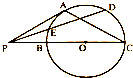 如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=
如图,P是⊙O外一点,PA是切线,割线PBC经过圆心O,且PB=