题目内容
数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n≥1).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)在数列{bn}中,bn=an•log3an,求数列{bn}的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)在数列{bn}中,bn=an•log3an,求数列{bn}的前n项和.
考点:数列的求和
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)根据an与Sn的关系,即可求数列{an}的通项公式;
(Ⅱ)求出数列{bn}的通项公式,利用错位相减法即可求数列{bn}的前n项和.
(Ⅱ)求出数列{bn}的通项公式,利用错位相减法即可求数列{bn}的前n项和.
解答:
解:( I)∵an+1=2Sn+1(n≥1),∴an=2Sn-1+1(n≥2),
∴an+1-an=2an,即an+1=3an(n≥2),
又a1=1,a2=2a1+1=3,
∴a2=3a1,∴an+1=3an(n∈N*).
∵a1=1,∴数列{an}是首项为1,公比为3的等比数列,
∴an=3n-1(n∈N*).
( II)∵bn=an•log3an=(n-1)•3n-1,
∴Sn=b1+b2+…+bn=0•30+1•31+…+(n-1)•3n-1
∴3Sn=0•31+1•32+…+(n-2)•3n-1+(n-1)•3n,
∴-2Sn=31+32+…+3n-1-(n-1)•3n,
∴-2Sn=
-(n-1)•3n=(
-n)•3n-
,
∴Sn=(
-
)•3n+
.
∴an+1-an=2an,即an+1=3an(n≥2),
又a1=1,a2=2a1+1=3,
∴a2=3a1,∴an+1=3an(n∈N*).
∵a1=1,∴数列{an}是首项为1,公比为3的等比数列,
∴an=3n-1(n∈N*).
( II)∵bn=an•log3an=(n-1)•3n-1,
∴Sn=b1+b2+…+bn=0•30+1•31+…+(n-1)•3n-1
∴3Sn=0•31+1•32+…+(n-2)•3n-1+(n-1)•3n,
∴-2Sn=31+32+…+3n-1-(n-1)•3n,
∴-2Sn=
| 3×(1-3n-1) |
| 1-3 |
| 3 |
| 2 |
| 3 |
| 2 |
∴Sn=(
| n |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题主要考查等比数列的应用,考查数列求和,要求熟练掌握错位相减法进行求和,考查学生的运算能力.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
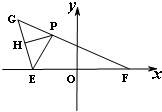 如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|=
如图,在平面直角坐标系中,点E,F是x轴上的两个定点,|EO|=|OF|= 如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在CE上,无论点F运动到何处时,总有BF⊥AE.
如图,四边形ABCD是边长为2的正方形,△ABE为等腰三角形,AE=BE,平面ABCD⊥平面ABE,动点F在CE上,无论点F运动到何处时,总有BF⊥AE.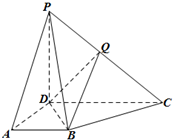 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=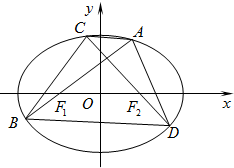 已知椭圆
已知椭圆