题目内容

已知函数f（x）=log5
1+x
1-x
．
（1）求f（x）的定义域；
（2）证明f（x）在定义域内是单调递增函数；
（3）解不等式：f（x）＜f（1-x）．（提示：若ab（或
a
b
）＞0，则有
a＞0
b＞0
或
a＜0
b＜0
）
考点：对数函数图象与性质的综合应用
专题：函数的性质及应用
分析：（1）由
1+x
1-x
＞0，求得函数f（x）的定义域为（-1，1）．
（2）先求导，利用导数历来判断函数的单调性．
（3）利用函数的单调性，列出不等式，解出即可．
解答： 解：（1）∵
1+x
1-x
＞0，
∴即-1＜x＜1
∴函数f（x）的定义域（-1，1）．
（2）∵f（x）=log5
1+x
1-x
．
∴f′（x）=
1
1+x
1-x
•ln5
•
2
(1-x)2
=
2
(1-x2)ln5
＞0，
∴f（x）在定义域内是单调递增函数
（3）由f（x）＜f（1-x）得，
log5
1+x
1-x
＜log5
2-x
x
．
由于f（x）是增函数
∴
1+ x
1-x
＜
2-x
x
，
解得，x＜
1
2

∴0＜x＜
1
2
点评：本题考查了对数的函数的定义域单调性和不等式的解法，属于中档题．
练习册系列答案
相关题目
已知函数f（x）=3-2log2x，g（x）=log2x
（1）如果x∈[1，2]，求函数h（x）=[f（x）+1]g（x）的值域；
（2）求函数M（x）=
f(x)+g(x)-|f(x)-g(x)|
2
的最大值．
（3）如果对任意x∈[1，2]，不等式f（x2）f（
x
）＞k•g（x）恒成立，求实数k的取值范围．
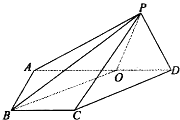如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA⊥PD，底面ABCD是直角梯形，其中BC∥AD，∠BAD=90°，AD=3BC，O是AD上一点．
（Ⅰ）若AD=3OD，求证：CD∥平面PBO；
（Ⅱ）求证：平面PAB⊥平面PCD．
已知函数f（x）=loga（x+1）-loga（1-x），a＞0且a≠1
（1）求函数f（x）的定义域；
（2）判断f（x）的奇偶性并予以证明；
（3）当a＞1时，求使f（x）＜0成立的x的取值范围．
数列{an}的前n项和为Sn，a1=1，an+1=2Sn+1（n≥1）．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）在数列{bn}中，bn=an•log3an，求数列{bn}的前n项和．
已知函数y=f（x）定义在实数集上，且对任意x，y∈R均有f（x+y）=f（x）+f（y），又对任意的x＞0，都有f（x）＜0，f（3）=-3．
（1）判断函数y=f（x）的奇偶性．
（2）证明函数y=f（x）在R上为单调减函数．
（3）试求函数y=f（x）在[m，n]（m，n∈Z，且mn＜0）上的值域．
某两个变量x和y之间的关系如下对应的数据：（精确到0.1）
x 3 5 6 7 9
y 2 3 3 4 5
（1）画出散点图；          
（2）求出回归方程；        
（3）若x=18，估计y的值．
参考公式：回归直线的方程是：
∧
y
=bx+a，其中b=
n
i=1
(xi-
.
x
)(yi-
.
y
)
n
i=1
(xi-
.
x
)2
=
n
i=1
xiyi-n
.
xy
n
i=1
xi2-n
.
x
2
，a=
.
y
-b
.
x
；对应的回归估计值．
已知数列{an}前n项的和为Sn，a1=1，an+an+1=2n-1，则S49=
 
．
F1、F2是椭圆
x2
25
+
y2
9
=1的左右两焦点，点P在椭圆上，若P到F1的距离等于8，则P到F2的距离是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网