题目内容
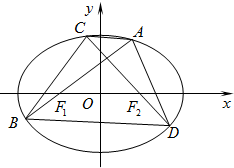 已知椭圆
已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)求四边形ACBD的面积S的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由椭圆
+
=1(a>b>0)的离心率为
,得到椭圆方程为
+
=1,将点P(1,
)代入椭圆方程,能求出椭圆方程为
+
=1.
(Ⅱ)当l1,l2中有一条直线的斜率不存在时,四边形的面积为S=6;若l1 与l2的斜率都存在,设l1的斜率为k,则l2的斜率为-
,直线l2的方程为y=k(x+1),设A(x1,y1),B(x2,y2),联立
,得|AB|=
,用-
代替k,得|CD|=
,由此能求出四边形ABCD面积的S∈[
,6].
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| x2 |
| 4c2 |
| y2 |
| 3c2 |
| 3 |
| 2 |
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)当l1,l2中有一条直线的斜率不存在时,四边形的面积为S=6;若l1 与l2的斜率都存在,设l1的斜率为k,则l2的斜率为-
| 1 |
| k |
|
| 12(k2+1) |
| 4k2+3 |
| 1 |
| k |
| 12(k2+1) |
| 3k2+4 |
| 288 |
| 49 |
解答:
解:(Ⅰ)∵椭圆
+
=1(a>b>0)的离心率为
,
且经过点P(1,
),
∴
=
,即a=2c,∴a2=4c2,b2=3c2,…(2分)
∴椭圆方程为
+
=1,
将点P(1,
)代入椭圆方程,得:
+
=1,
解得c2=1,…(4分)
∴所求椭圆方程为
+
=1.…(5分)
(Ⅱ)当l1,l2中有一条直线的斜率不存在,则另一条直线的斜率为0,
此时四边形的面积为S=6,…(7分)
若l1 与l2的斜率都存在,设l1的斜率为k,则l2的斜率为-
.
∴直线l2的方程为y=k(x+1),
设A(x1,y1),B(x2,y2),联立
,
消去y整理得,(4k2+3)x2-8k2x+4k2-12=0,(1)
∴x1+x2=
,x1 x2=
,…(8分)
∴|x1-x2|=
,∴|AB|=
•|x1-x2|=
,(2)…(9分)
注意到方程(1)的结构特征,或图形的对称性,
可以用-
代替(2)中的k,得|CD|=
,…(10分)
∴S=
|AB|•|CD|=
,令k2=t∈(0,+∞),
∴S=
=
=6-
≥6-
=
,
∴S∈[
,6),
综上可知,四边形ABCD面积的S∈[
,6].…(13分)
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
且经过点P(1,
| 3 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
∴椭圆方程为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
将点P(1,
| 3 |
| 2 |
| 1 |
| 4c2 |
| ||
| 3c2 |
解得c2=1,…(4分)
∴所求椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)当l1,l2中有一条直线的斜率不存在,则另一条直线的斜率为0,
此时四边形的面积为S=6,…(7分)
若l1 与l2的斜率都存在,设l1的斜率为k,则l2的斜率为-
| 1 |
| k |
∴直线l2的方程为y=k(x+1),
设A(x1,y1),B(x2,y2),联立
|
消去y整理得,(4k2+3)x2-8k2x+4k2-12=0,(1)
∴x1+x2=
| 8k2 |
| 4k2+3 |
| 4k2-12 |
| 4k2+3 |
∴|x1-x2|=
12
| ||
| 4k2+3 |
| 1+k2 |
| 12(k2+1) |
| 4k2+3 |
注意到方程(1)的结构特征,或图形的对称性,
可以用-
| 1 |
| k |
| 12(k2+1) |
| 3k2+4 |
∴S=
| 1 |
| 2 |
| 72(1+k2)2 |
| (4k2+3)•(3k2+4) |
∴S=
| 72(1+t)2 |
| (4t+3)(3+4) |
| 6(12t2+25t+12)-6t |
| 12t2+25t+12 |
=6-
| 6 | ||
12t+
|
| 6 |
| 49 |
| 288 |
| 49 |
∴S∈[
| 288 |
| 49 |
综上可知,四边形ABCD面积的S∈[
| 288 |
| 49 |
点评:本题考查椭圆的标准方程的求法,考查四边形面积的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目

