题目内容
求函数y=log2[3-2
tanx-3tan2x]的定义域与值域．
| 3 |
考点：对数函数图象与性质的综合应用
专题：函数的性质及应用
分析：由题意可得3-2
tanx-3tan2x＞0，解得-
＜tanx＜
，可得定义域．令u=3-2
tanx-3tan2x=-3(tanx+
)2+4，利用二次函数的性质求得u的范围，可得函数y=log2u 的值域．
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
解答：
解：由题意可得 3-2
tanx-3tan2x＞0，解得-
＜tanx＜
，
∴函数的定义域为（kπ-
，kπ+
），k∈z．
令u=3-2
tanx-3tan2x=-3(tanx+
)2+4，
利用二次函数的性质求得u∈（0，4]，故函数y=log2u 的值域为（-∞，2]．
| 3 |
| 3 |
| ||
| 3 |
∴函数的定义域为（kπ-
| π |
| 3 |
| π |
| 6 |
令u=3-2
| 3 |
| ||
| 3 |
利用二次函数的性质求得u∈（0，4]，故函数y=log2u 的值域为（-∞，2]．
点评：本题主要考查对数函数的图象和性质应用，二次函数的性质，体现了转化的数学思想，属于中档题．
练习册系列答案
计算高手系列答案
相关题目
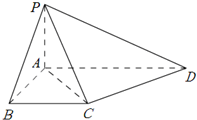如图，在四棱锥P-ABCD，PA⊥平面ABCD，PA=AB=BC=