题目内容
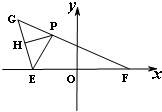如图，在平面直角坐标系中，点E，F是x轴上的两个定点，|EO|=|OF|=| 3 |
| HP |
| EG |
（Ⅰ）求点P的轨迹方程；
（Ⅱ）若直线l：y=kx+2与点P的轨迹有两个不同的交点A，B，且
| OA |
| OB |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（Ⅰ）由已知条件推导出点P的轨迹是以E，F焦点的椭圆，由已知条件推导出点P的轨迹方程．
（Ⅱ）由
，整理得（1+4k2）x2+16kx+12=0，由此利用已知条件能求出实数k的取值范围．
（Ⅱ）由
|
解答：
解：（Ⅰ）由
•
=0，得
⊥
，
又H为GE中点，∴|PE|=|PG|，
∴|PE|+|PF|=|PG|+|PF|=|GF|=4，
∴点P的轨迹是以E，F焦点的椭圆，
且a=2，c=
，b=
=1，
∴点P的轨迹方程为
+y2=1（6分）
（Ⅱ）由
，整理得（1+4k2）x2+16kx+12=0，
设A（x1，y1），B（x2，y2），
则有x1+x2=
，x1x2=
①，
且△=16（4k2-3）＞0，（8分）
若
•
＞0，则x1x2+y1y2＞0，
即x1x2+（kx1+2）（kx2+2）＞0，
整理得（1+k2）x1x2+2k（x1+x2）+4＞0，
再将①代入，得：(1+k2)
-2k
+4＞0，
整理k2-4＜0，（10分）
又∵△＞0，∴
＜k2＜4，
∴实数k的取值范围是{k|-2＜k＜-
或
＜k＜2}．（12分）
| HP |
| EG |
| HP |
| EG |
又H为GE中点，∴|PE|=|PG|，
∴|PE|+|PF|=|PG|+|PF|=|GF|=4，
∴点P的轨迹是以E，F焦点的椭圆，
且a=2，c=
| 3 |
| a2-c2 |
∴点P的轨迹方程为
| x2 |
| 4 |
（Ⅱ）由
|
设A（x1，y1），B（x2，y2），
则有x1+x2=
| -16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
且△=16（4k2-3）＞0，（8分）
若
| OA |
| OB |
即x1x2+（kx1+2）（kx2+2）＞0，
整理得（1+k2）x1x2+2k（x1+x2）+4＞0，
再将①代入，得：(1+k2)
| 12 |
| 1+4k2 |
| 16 |
| 1+4k2 |
整理k2-4＜0，（10分）
又∵△＞0，∴
| 3 |
| 4 |
∴实数k的取值范围是{k|-2＜k＜-
| ||
| 2 |
| ||
| 2 |
点评：本题考查点的轨迹方程的求法，考查实数的取值范围的求法，解题时要认真审题，注意函数与方程思想的合理运用．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
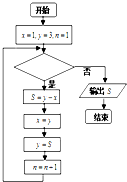已知数列{an}满足a1=1，a2=3，an+2=an+1-an，n∈N*，利用如图所示的程序框图计算该数列的第n项（n≥3），若输出S的结果为1，则判断框内的条件可能是（ ）| A、n≤5？ | B、n≤6？ |
| C、n≤7？ | D、n≤8？ |
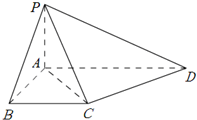如图，在四棱锥P-ABCD，PA⊥平面ABCD，PA=AB=BC=