题目内容
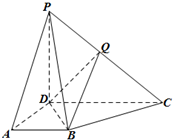 在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=
在四棱锥P-ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=| π |
| 2 |
| PQ |
| PC |
考点:用空间向量求平面间的夹角
专题:空间角
分析:以D为原点,DA、DC、DP分别为x,y,z轴,建立空间直角坐标系,利用向量法能确定λ的值,使得二面角Q-BD-P为45°.
解答:
解:∵侧面PCD⊥底面ABCD,平面PCD∩ABCD=CD,PD⊥CD,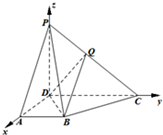
∴PD⊥平面ABCD,
∴PD⊥AD,即DA、DC、DP两两垂直,
如图,以D为原点,DA、DC、DP分别为x,y,z轴,
建立空间直角坐标系,
∵AB=AD=PD=1,CD=2,
∴D(0,0,0),B(1,1,0),P(0,0,1),C(0,2,0),
∴
=(1,1,0),
=(0,0,1),
=(0,2,-1),
设平面PBD的一个法向量为
=(x,y,z),
则
,取x=-1,得
=(-1,1,0),
设
=λ
=(0,2λ,-λ),λ∈(0,1),
则Q(0,2λ,1-λ),
=(0,2λ,1-λ),
设平面QBD的一全法向量
=(a,b,c),
则
,
取x=-1,得
=(-1,1,
),
∵二面角Q-BD-P为45°,
∴cos45°=
=
=
,
由λ∈(0,1),解得λ=
-1.

∴PD⊥平面ABCD,
∴PD⊥AD,即DA、DC、DP两两垂直,
如图,以D为原点,DA、DC、DP分别为x,y,z轴,
建立空间直角坐标系,
∵AB=AD=PD=1,CD=2,
∴D(0,0,0),B(1,1,0),P(0,0,1),C(0,2,0),
∴
| DB |
| DP |
| PC |
设平面PBD的一个法向量为
| n |
则
|
| n |
设
| PQ |
| PC |
则Q(0,2λ,1-λ),
| DQ |
设平面QBD的一全法向量
| m |
则
|
取x=-1,得
| m |
| 2λ |
| λ-1 |
∵二面角Q-BD-P为45°,
∴cos45°=
|
| ||||
|
|
| 2 | ||||||
|
| ||
| 2 |
由λ∈(0,1),解得λ=
| 2 |
点评:本题考查使得二面角为45°的点的位置的确定,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
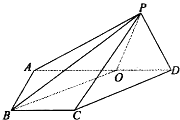 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.