题目内容
已知a=0.3-0.2，b=log0.50.8，c=log0.53，那么a，b，c的大小关系是（ ）
| A、a＜b＜c |
| B、c＜b＜a |
| C、c＜a＜b |
| D、a＜c＜b |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数函数的单调性即可得出．
解答：
解：∵a=0.3-0.2＞0.30=1，
0=log0.51＜b=log0.50.8＜log0.50.5=1，
c=log0.53＜log0.51=0，
∴a＞b＞c．
故选：C．
0=log0.51＜b=log0.50.8＜log0.50.5=1，
c=log0.53＜log0.51=0，
∴a＞b＞c．
故选：C．
点评：本题考查了对数函数的单调性，属于基础题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
将函数f（x）=sinx图象所有的点向右移动
个单位长度，再将所得各点的横坐标缩短到原来的
倍（纵坐标不变），所得图象的函数解析式为（ ）
| π |
| 3 |
| 1 |
| 2 |
A、y=sin（
| ||||
B、y=sin（
| ||||
C、y=sin（2x-
| ||||
D、y=sin（2x-
|
已知a=7log23.4，b=7log43.6，c=（
） lo
，比较a，b，c的大小（ ）
| 1 |
| 7 |
| g | 0.3 3 |
| A、a＜b＜c |
| B、b＜a＜c |
| C、b＜c＜a |
| D、c＜a＜b |
如图所示是某一几何体的三视图，则它的体积为（ ）
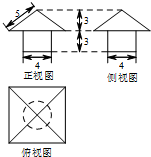
| A、16+12π |
| B、48+12π |
| C、64+12π |
| D、64+16π |
若变量x，y满足约束条件
且z=4y-x的最大值为a，最小值为b，则a+b的值是（ ）
|
| A、4 | B、20 | C、10 | D、12 |
设f（x）=ax2+bx+c（a，b，c∈R），e为自然对数的底数．若f′（x）lnx＞
．则（ ）
| f(x) |
| x |
| A、f（2）＜f（e）ln2，2f（e）＞f（e2） |
| B、f（2）＜f（e）ln2，2f（e）＜f（e2） |
| C、f（2）＞f（e）ln2，2f（e）＜f（e2） |
| D、f（2）＞f（e）ln2，2f（e）＞f（e2） |
圆C：（x+1）2+（y-3）2=9上有两点P，Q关于直线x+my+4=0对称，则m等于（ ）
A、-
| ||
B、
| ||
| C、-1 | ||
| D、1 |