题目内容
若圆C过点(0,1)且与直线l:y=-1相切,设圆心C的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)记F(0,1),是否存在正数m,对于过点M(0,M)且与曲线E有两个交点A、B的任一直线,都有
•
<0,若存在,求出m的取值范围,若不存在,请说明理由.
(Ⅰ)求曲线E的方程;
(Ⅱ)记F(0,1),是否存在正数m,对于过点M(0,M)且与曲线E有两个交点A、B的任一直线,都有
| FA |
| FB |
考点:轨迹方程,平面向量数量积的运算
专题:向量与圆锥曲线
分析:(Ⅰ)由点C到定点M的距离等于到定直线l的距离与抛物线的定义可得点C的轨迹为抛物线所以曲线E的方程为x2=4y;
(Ⅱ)首先由于过点M(0,m)的直线与开口向上的抛物线有两个交点A、B,则设该直线的方程为y=kx+m,然后与抛物线方程联立方程组,进而通过消元转化为一元二次方程;再根据韦达定理及向量的数量积公式,实现
•
<0的等价转化;最后通过m、k的不等式求解m的取值范围.
(Ⅱ)首先由于过点M(0,m)的直线与开口向上的抛物线有两个交点A、B,则设该直线的方程为y=kx+m,然后与抛物线方程联立方程组,进而通过消元转化为一元二次方程;再根据韦达定理及向量的数量积公式,实现
| FA |
| FB |
解答:
解:(Ⅰ)依题意,点C到定点M的距离等于到定直线l的距离,所以点C的轨迹为抛物线,曲线E的方程为x2=4y;
(Ⅱ)设过点M(0,m)(m>0)的直线l与曲线E的交点为A(x1,y1),B(x2,y2).
设l的方程为y=kx+m,由
,得x2-4kx-4m=0,
于是x1+x2=4k,x1x2=-4m ①
又
=(x1,y1-1),
=(x2,y2-1).
则
•
<0?x1•x2+(y1-1)(y2-1)=x1x2-(y1+y2)+1+y1y2<0 ②
又y1=kx1+m,y2=kx2+m,于是不等式②等价于(k2+1)x1x2+k(m-1)(x1+x2)+m2-2m+1<0 ③
由①式,不等式③等价于m2-6m+1-4k2<0 ④
要使④成立,则m2-6m+1<4k2,
∵4k2≥0,
若使该式对任意实数k都成立,则m2-6m+1<0,
解得:3-2
<m<3+2
.
(Ⅱ)设过点M(0,m)(m>0)的直线l与曲线E的交点为A(x1,y1),B(x2,y2).
设l的方程为y=kx+m,由
|
于是x1+x2=4k,x1x2=-4m ①
又
| FA |
| FB |
则
| FA |
| FB |
又y1=kx1+m,y2=kx2+m,于是不等式②等价于(k2+1)x1x2+k(m-1)(x1+x2)+m2-2m+1<0 ③
由①式,不等式③等价于m2-6m+1-4k2<0 ④
要使④成立,则m2-6m+1<4k2,
∵4k2≥0,
若使该式对任意实数k都成立,则m2-6m+1<0,
解得:3-2
| 2 |
| 2 |
点评:本题综合考查向量知识、直线与抛物线的相交问题及代数运算能力,是中档题.

练习册系列答案
相关题目
m=0是方程x2+y2-4x+2y+m=0表示圆的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
若F(c,0)是双曲线
-
=1(a>b>0)的右焦点,过F作该双曲线一条渐近线的垂线与两条渐近线交于A,B两点,O为坐标原点,△OAB的面积为
,则该双曲线的离心率e=( )
| x2 |
| a2 |
| y2 |
| b2 |
| 12a2 |
| 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知数列{an}满足a1=1,
=n,n∈N*,设数列{
}的前n项和为Sn,则Sn的取值范围是( )
| an+1-an |
| an |
| n |
| an+1 |
| A、(0,1) | ||
B、[
| ||
C、[
| ||
| D、(1,+∞) |
若命题“p或q”为真,“非p”为真,则( )
| A、p真q真 | B、p假q真 |
| C、p真q假 | D、p假q假 |
双曲线
-
=1(a>0,b>0)的渐近线与圆x2+(y-2)2=1相切,则双曲线离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
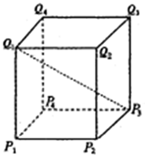 若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,集合M={x|x=
若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,集合M={x|x=