题目内容
以下命题中真命题的个数为( )
①p:?x∈R,x2+2x+2=0的否定;
②?x∈N,x3>x2;
③若p:?x∈M,p(x),则¬p:?x∈M,¬p(x)
①p:?x∈R,x2+2x+2=0的否定;
②?x∈N,x3>x2;
③若p:?x∈M,p(x),则¬p:?x∈M,¬p(x)
| A、0 | B、1 | C、2 | D、3 |
考点:命题的否定
专题:简易逻辑
分析:①写出命题p:?x∈R,x2+2x+2=0的否定,再判断即可;
②举例x=0∈N,03=02=0,说明②?x∈N,x3>x2,错误;
③利用全称命题的否定为特称命题,即可判断③若p:?x∈M,p(x)的否定为:¬p:?x∈M,¬p(x).
②举例x=0∈N,03=02=0,说明②?x∈N,x3>x2,错误;
③利用全称命题的否定为特称命题,即可判断③若p:?x∈M,p(x)的否定为:¬p:?x∈M,¬p(x).
解答:
解:①p:?x∈R,x2+2x+2=0的否定为:¬p:?x∈R,x2+2x+2=(x+1)2+1≠0,正确;
②?x∈N,x3>x2,错误;如x=0∈N,03=02=0,故②错误;
③若p:?x∈M,p(x),则¬p:?x∈M,¬p(x),正确.
故选:C.
②?x∈N,x3>x2,错误;如x=0∈N,03=02=0,故②错误;
③若p:?x∈M,p(x),则¬p:?x∈M,¬p(x),正确.
故选:C.
点评:本题考查命题的真假判断与应用,着重考查全称命题与特称命题的关系及应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若f(x)=(m-1)x2+2mx+3为偶函数,则f(x)在区间(-7,-2)上是( )
| A、减函数 | B、先减后增函数 |
| C、增函数 | D、先增后减函数 |
已知函数y=f(x+1)定义域是[-2,3],则y=f(2x-1)的定义域( )
A、[0,
| ||
| B、[-1,4] | ||
| C、[-5,5] | ||
| D、[-3,7] |
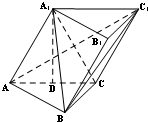 如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.
如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.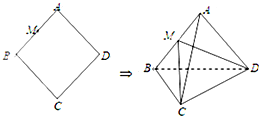 在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为