题目内容
过点M(1,1)作斜率为-
的直线与椭圆C:
+
=1(a>b>0)相交于A,B,若M是线段AB的中点,则椭圆C的离心率为( )
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:利用点差法,结合M是线段AB的中点,斜率为-
,即可求出椭圆C的离心率.
| 1 |
| 2 |
解答:
解:设A(x1,y1),B(x2,y2),则
,
∵过点M(1,1)作斜率为-
的直线与椭圆C:
+
=1(a>b>0)相交于A,B两点,
M是线段AB的中点,
∴两式相减可得
+(-
)•
=0,
∴a=
b,
∴c=
=b,
∴e=
=
.
故选:A.
|
∵过点M(1,1)作斜率为-
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
M是线段AB的中点,
∴两式相减可得
| 2 |
| a2 |
| 1 |
| 2 |
| 2 |
| b2 |
∴a=
| 2 |
∴c=
| a2-b2 |
∴e=
| c |
| a |
| ||
| 2 |
故选:A.
点评:本题考查椭圆C的离心率的求法,考查学生的计算能力,正确运用点差法是解题的关键.

练习册系列答案
相关题目
已知集合A={x|
≥1},B={x|y=
},则A∪B=( )
| 1 |
| x+1 |
| x2-1 |
| A、(-∞,1] |
| B、(-1,0)∪[1,+∞) |
| C、(-∞,0)∪[1,+∞) |
| D、(-∞,0]∪[1,+∞) |
设l、m是两条不同的直线,α、β是两个不同的平面,则下列论述正确的是( )
| A、若l∥α,m∥α,则l∥m |
| B、若l∥α,l∥β,则α∥β |
| C、若l∥m,l⊥α,则m⊥α |
| D、若l∥α,α⊥β,则l⊥β |
函数y=ln(2x-1)的导数是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知a∈R,则“a≥0”是“函数f(x)=x2+|x-a|在(-∞,0]上是减函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在△ABC中,角A,B,C所对的边分别为a,b,c,若A=30°且b=
a,则角C等于( )
| 3 |
| A、30° | B、60° |
| C、90° | D、30°或90° |
A,B,C,D这4名学生参加甲、乙、丙三所高校的自主招生考试,每人限报一所学校,每校至少一人参加,则学生A参加甲高校且学生B参加乙高校考试的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
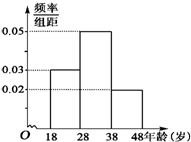 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表: