题目内容
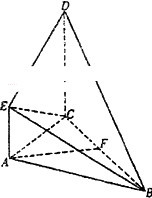 如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.(Ⅰ)求证:平面BCD⊥平面ABC;
(Ⅱ)求证:AF∥平面BDE;
(Ⅲ)求直线BE与平面BCD所成角的正弦值.
考点:平面与平面垂直的判定,直线与平面平行的判定,直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)由已知条件推导出DC⊥面ABC,由此能证明平面BCD⊥平面ABC.
(Ⅱ)取BD的中点P,连结EP、FP,由已知条件推导出四边形AFPE是平行四边形,由此能证明AF∥面BDE.
(Ⅲ)∠EBP是直线BE与平面BCD所成角,由此能求出其正弦值.
(Ⅱ)取BD的中点P,连结EP、FP,由已知条件推导出四边形AFPE是平行四边形,由此能证明AF∥面BDE.
(Ⅲ)∠EBP是直线BE与平面BCD所成角,由此能求出其正弦值.
解答:
(Ⅰ)证明:∵面ABC⊥面ACDE,
面ABC∩面ACDE=AC,CD⊥AC,
∴DC⊥面ABC,
又∵DC?面BCD,∴平面BCD⊥平面ABC.
(Ⅱ)证明:取BD的中点P,连结EP、FP,则FP
DC,
又∵EA
DC,∴EA
FP,
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP?面BDE且AF?面BDE,∴AF∥面BDE.
(Ⅲ)解:∵DC⊥面ABC,∴DC⊥AF,
∵等腰直角△ABC,F为BC的中点,
∴AF⊥BC,∵DC交BC于C,∴AF⊥面BCD,
又AF∥EP,∴EP⊥面BCD,
∴∠EBP即为所求,
∴sin∠EBP=
.
面ABC∩面ACDE=AC,CD⊥AC,
∴DC⊥面ABC,
又∵DC?面BCD,∴平面BCD⊥平面ABC.
(Ⅱ)证明:取BD的中点P,连结EP、FP,则FP
| ∥ |
. |
| 1 |
| 2 |
又∵EA
| ∥ |
. |
| 1 |
| 2 |
| ∥ |
. |
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP?面BDE且AF?面BDE,∴AF∥面BDE.
(Ⅲ)解:∵DC⊥面ABC,∴DC⊥AF,
∵等腰直角△ABC,F为BC的中点,
∴AF⊥BC,∵DC交BC于C,∴AF⊥面BCD,
又AF∥EP,∴EP⊥面BCD,
∴∠EBP即为所求,
∴sin∠EBP=
| ||
| 5 |
点评:本题考查平面与平面垂直的证明,考查直线与平面平行的证明,考查二面角正弦值的求法,解题时要认真审题,注意空间思维能力的合理运用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
设l、m是两条不同的直线,α、β是两个不同的平面,则下列论述正确的是( )
| A、若l∥α,m∥α,则l∥m |
| B、若l∥α,l∥β,则α∥β |
| C、若l∥m,l⊥α,则m⊥α |
| D、若l∥α,α⊥β,则l⊥β |
在△ABC中,角A,B,C所对的边分别为a,b,c,若A=30°且b=
a,则角C等于( )
| 3 |
| A、30° | B、60° |
| C、90° | D、30°或90° |
A,B,C,D这4名学生参加甲、乙、丙三所高校的自主招生考试,每人限报一所学校,每校至少一人参加,则学生A参加甲高校且学生B参加乙高校考试的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,直三棱柱ABC-A1B1C1底面边长均为
如图,直三棱柱ABC-A1B1C1底面边长均为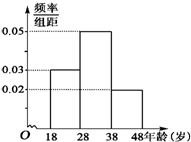 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表: 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程).被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300],绘制成如图所示的频率分布直方图.