题目内容
定义在R上的函数f(x)满足以下两个条件:
①对任意的x,y∈R,f(x-y+1)=f x)f(y)+f(1-x)f(1-y);
②f(x)在区间[0,1]上单调递增;
(1)求f(0);
(2)求证:f(x)是图象关于直线x=1对称的奇函数;
(3)求不等式的解集f(x)≥
的解集.
①对任意的x,y∈R,f(x-y+1)=f x)f(y)+f(1-x)f(1-y);
②f(x)在区间[0,1]上单调递增;
(1)求f(0);
(2)求证:f(x)是图象关于直线x=1对称的奇函数;
(3)求不等式的解集f(x)≥
| 1 |
| 2 |
考点:抽象函数及其应用
专题:计算题,函数的性质及应用
分析:(1)令x=y=0,再令x=0,y=
,讨论f(
)是否为0,即可求出f(0),f(1);
(2)用y代替1-y,再令y=-x,即可得到f(x+1)=f(1-x),再代入f(0)=f(x)f(1+x)+f(1-x)f(-x,即可得证;
(3)令x=y=
,再由(2)即可得到f(x+4)=f(x),f(x)为周期为4的函数,由f(
)=
,即可解出不等式f(x)≥
.
| 1 |
| 2 |
| 1 |
| 2 |
(2)用y代替1-y,再令y=-x,即可得到f(x+1)=f(1-x),再代入f(0)=f(x)f(1+x)+f(1-x)f(-x,即可得证;
(3)令x=y=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)令x=y=0则f(1)=f2(0)+f2(1)①
再令x=0,y=
可得f(
)=f(0)f(
)+f(1)f(
)
若f(
)=0则f(1)=f2(
)+f2(
)=0这与f (x)在区间[0,1]上单调递增矛盾,
∴f(
)≠0故1=f(0)+f(1)②
由①、②解得
或
(舍),
综上可知
;
(2)用y代替1-y得f(x+y)=f(x)f(1-y)+f(1-x)f(y)③
在③式中令y=-x可得f(0)=f(x)f(1+x)+f(1-x)f(-x)④
由③式可知f(x+1)=f(x)f(0)+f(1-x)f(1)
=f(x)•0+f(1-x)•1=f(1-x)
即f(x+1)=f(1-x),所以f(x)的图象关于直线x=1对称,
将上式代入④得0=f(x)f(1+x)+f(1+x)f(-x)
又因为f(x+1)不恒为0∴f(x)+f(-x)=0恒成立,故f(x)为奇函数,得证.
(3)在③中令
另一方面,由f(x)为奇函数及f(x+1)=f(1-x)
可知f(x+1)=-f(x-1)∴f(x+2)=-f(x),
∴f(x+4)=f(x)
即解集为{x|4k+
≤x≤4k+
,k∈Z}.
再令x=0,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
若f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(
| 1 |
| 2 |
由①、②解得
|
|
综上可知
|
(2)用y代替1-y得f(x+y)=f(x)f(1-y)+f(1-x)f(y)③
在③式中令y=-x可得f(0)=f(x)f(1+x)+f(1-x)f(-x)④
由③式可知f(x+1)=f(x)f(0)+f(1-x)f(1)
=f(x)•0+f(1-x)•1=f(1-x)
即f(x+1)=f(1-x),所以f(x)的图象关于直线x=1对称,
将上式代入④得0=f(x)f(1+x)+f(1+x)f(-x)
又因为f(x+1)不恒为0∴f(x)+f(-x)=0恒成立,故f(x)为奇函数,得证.
(3)在③中令
|
另一方面,由f(x)为奇函数及f(x+1)=f(1-x)
可知f(x+1)=-f(x-1)∴f(x+2)=-f(x),
∴f(x+4)=f(x)
|
即解集为{x|4k+
| 1 |
| 3 |
| 5 |
| 3 |
点评:本题主要考查函数的性质和运用,考查函数的单调性、周期性和奇偶性及运用,同时考查解决抽象函数的常用方法:赋值法,是一道综合题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
函数y=ln(2x-1)的导数是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
A,B,C,D这4名学生参加甲、乙、丙三所高校的自主招生考试,每人限报一所学校,每校至少一人参加,则学生A参加甲高校且学生B参加乙高校考试的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
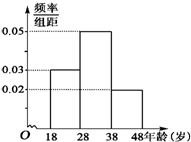 武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表:
武汉电视台为了宣传武汉城市圈的情况,特举办了一期有奖知识问答活动,活动对18~48岁的人群随机抽取n人回答问题“武汉城市圈包括哪几个城市”,统计数据结果如表: 在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=
在长方体ABCD-A1B1C1D1中,AD=AA1=3,AB=