题目内容
已知曲线C的参数方程为
(θ是参数),以原点O为极点,以x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为θ=
(ρ∈R),曲线C与直线l相交于点A、B.
(Ⅰ) 将曲线C的方程化为普通方程,直线l的极坐标方程化为直角坐标方程;
(Ⅱ) 求弦AB的长.
|
| π |
| 4 |
(Ⅰ) 将曲线C的方程化为普通方程,直线l的极坐标方程化为直角坐标方程;
(Ⅱ) 求弦AB的长.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(Ⅰ)由
转化为:(x-3)2+y2=9,直线l的极坐标方程为θ=
(ρ∈R),转化为;直线l的直角坐标方程是:x-y=0
(Ⅱ) 直线l的参数方程为
把它代入方程(x-3)2+y2=9中,弦AB的长为:|AB|=|t1-t2|=
=
=3
|
| π |
| 4 |
(Ⅱ) 直线l的参数方程为
|
| (t1+t2)2-4t1t2 |
| 18-0 |
| 2 |
解答:
解:(Ⅰ)由
可得:
,
把 ①2+②2得到原参数方程的普通方程:(x-3)2+y2=9,
直线l的极坐标方程为θ=
(ρ∈R),
由互化公式tanθ=
,即
=1,
则直线l的直角坐标方程是:x-y=0.
(Ⅱ) 直线l的参数方程为:
(t为参数),
把它代入方程(x-3)2+y2=9中,
即(
t-3)2+(
t)2=9⇒t2-3
t=0,
设点A、B对应的参数值分别为t1,t2,由参数t的几何意义可得,
弦AB的长为:|AB|=|t1-t2|=
=
=3
.
故答案为:(Ⅰ)(x-3)2+y2=9和x-y=0,
(Ⅱ)AB=3
.
|
|
把 ①2+②2得到原参数方程的普通方程:(x-3)2+y2=9,
直线l的极坐标方程为θ=
| π |
| 4 |
由互化公式tanθ=
| y |
| x |
| y |
| x |
则直线l的直角坐标方程是:x-y=0.
(Ⅱ) 直线l的参数方程为:
|
把它代入方程(x-3)2+y2=9中,
即(
| ||
| 2 |
| ||
| 2 |
| 2 |
设点A、B对应的参数值分别为t1,t2,由参数t的几何意义可得,
弦AB的长为:|AB|=|t1-t2|=
| (t1+t2)2-4t1t2 |
| 18-0 |
| 2 |
故答案为:(Ⅰ)(x-3)2+y2=9和x-y=0,
(Ⅱ)AB=3
| 2 |
点评:本题考查的知识要点:参数方程和直角坐标方程的互化及极坐标方程与直角坐标方程的互化,弦长公式的应用.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
下列四个方程中表示y是x的函数的是( )
①x-2y=6②x2+y=1③x+y2=1④x=
.
①x-2y=6②x2+y=1③x+y2=1④x=
| y |
| A、①② | B、①④ | C、③④ | D、①②④ |
设集合M={x|0≤x≤2},N={y|0≤y≤2},给出下列4个图形,其中能表示集合M到N的函数关系的有( )
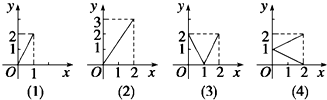

| A、0个 | B、1个 | C、2个 | D、3个 |
定义在(0,
)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
| π |
| 2 |
A、
| ||||||||
B、f(1)>2f(
| ||||||||
C、
| ||||||||
D、
|
设a=0.1
,b=log0.12,c=30.1,d=lg
,那么a,b,c,d的大小关系为( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、b>c>a>d |
| B、c>a>b>d |
| C、c>a>d>b |
| D、d>c>a>b |