题目内容

函数f（x）=sinπx+cosπx对任意的x∈R都有f（x1）≤f（x）≤f（x2）成立，则|x2-x1|的最小值为（　　）
A、
1
2
B、1
C、2
D、4
考点：三角函数的最值
专题：三角函数的求值
分析：由题意可得f（x1）为函数的最小值，f（x2）为函数的最大值，故|x2-x1|的最小值为半个周期，再根据正弦函数的周期性可得结论．
解答： 解：∵函数f（x）=sinπx+cosπx=
2
sin（πx+
π
4
），f（x1）≤f（x）≤f（x2），
可得f（x1）为函数的最小值，f（x2）为函数的最大值，故|x2-x1|的最小值为半个周期，
即
1
2
•
2π
π
=1，
故选：B．
点评：本题主要考查正弦函数的周期性和值域，属于基础题．
练习册系列答案
相关题目
某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：
年份2007200820092010201120122013
年份代号t1234567
人均纯收入y2.93.33.64.44.85.25.9
（Ⅰ）求y关于t的线性回归方程；（已知b=0.5）
（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．
下列四个方程中表示y是x的函数的是（　　）
①x-2y=6②x2+y=1③x+y2=1④x=
y
．
A、①②B、①④C、③④D、①②④
关于函数f（x）=4sin（2x+
π
3
），（x∈R）有下列命题：
①y=f（x）是以2π为最小正周期的周期函数； 
②y=f（x）可改写为y=4cos（2x-
π
6
）；
③y=f（x）的图象关于点（-
π
6
，0）对称；   
④y=f（x）的图象关于直线x=-
5π
12
对称；
⑤y=|f（x）|是以π为最小正周期的周期函数．
其中正确的序号为
 
．
已知点P（lga，lgb）关于x轴的对称点为（0，-1），则正数a、b的值分别为
 
．
已知函数f（x）=5sinxcosx-5
3
cos2x+
5
3
2
．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求f（x）的单调递增区间，并求出f（x）在[
π
3
，
5π
6
]上的最大值与最小值．
定义在（0，
π
2
）上的函数f（x），f′（x）是它的导函数，且恒有f（x）＜f′（x）tanx成立，则（　　）
A、
3
f（
π
4
）＞
2
f（
π
3
）
B、f（1）＞2f（
π
6
）•sin1
C、
2
f（
π
6
）＞f（
π
4
）
D、
3
f（
π
6
）＞f（
π
3
）
设f（x）=
x+3(x≥10)
f(f(x+5))(x≤10)
，则f（5）的值是（　　）
A、24B、21C、18D、16
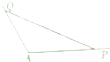如图，角A为钝角，且sinA=
3
5
，点P、Q分别是在角A的两边上不同于点A的动点．
（1）设∠APQ=α．∠AQP=β．且cosα=
12
13
．求sin（2α+β）的值；
（2）若PQ=3
5
，求△APQ面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网