Question

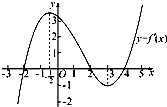如果函数y=f（x）的导函数的图象如图所示，给出下列判断：
①函数y=f（x）在区间(-3，-

1

2

)内单调递增；
②函数y=f（x）在区间(-

1

2

，3)内单调递减；
③函数y=f（x）在区间（4，5）内单调递增；
④当x=2时，函数y=f（x）有极小值；
⑤当x=-

1

2

时，函数y=f（x）有极大值．则上述判断中正确的是（　　）

• A、①②
• B、②③
• C、③④⑤
• D、③

Answer 1

考点：利用导数研究函数的极值

专题：函数的性质及应用,导数的综合应用

分析：利用使f′（x）＞0的区间是增区间，使f′（x）＜0的区间是减区间，分别对①②③进行逐一判定，导数等于零的值是极值，先增后减是极大值，先减后增是极小值，再对④⑤进行判定．

解答： 解：对于①，函数y=f（x）在区间（-3，-

1

2

）内有增有减，故①不正确；
对于②，函数y=f（x）在区间（-

1

2

，3）有增有减，故②不正确；
对于③，函数y=f（x）当x∈（4，5）时，恒有f′（x）＞0．故③正确；
对于④，当x=2时，函数y=f（x）有极大值，故④不正确；
对于⑤，当x=-

1

2

时，f′（x）≠0，故⑤不正确．
故选：D．

点评：本题考查了通过导函数图象判定原函数的单调性，以及极值问题，属于易错题．