题目内容
下列计算正确的是( )
| A、(-2a)2=2a2 |
| B、a6÷a3=a2 |
| C、-2(a-1)=2-2a |
| D、a•a2=a2 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:按照有理数的幂的有关运算法则解答.
解答:
解:对选项A,结果应该为4a2;
对选项B,结果应该为a6-3=a3;
对选项C,正确;
对选项D,结果应该为:a1+2=a3;
故选C.
对选项B,结果应该为a6-3=a3;
对选项C,正确;
对选项D,结果应该为:a1+2=a3;
故选C.
点评:本题考查了有理数 幂的相关运算,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
定义在(0,
)上的函数f(x),f′(x)是它的导函数,且恒有f(x)<f′(x)tanx成立,则( )
| π |
| 2 |
A、
| ||||||||
B、f(1)>2f(
| ||||||||
C、
| ||||||||
D、
|
设a=0.1
,b=log0.12,c=30.1,d=lg
,那么a,b,c,d的大小关系为( )
| 1 |
| 3 |
| 1 |
| 3 |
| A、b>c>a>d |
| B、c>a>b>d |
| C、c>a>d>b |
| D、d>c>a>b |
等比数列{an}中,a1a3a5=8,则a3=( )
| A、1 | B、2 | C、3 | D、4 |
设f(x)=
,则f(f(-1))=( )
|
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
集合A={x∈N|-4<x-1<4,且x≠1}的真子集的个数为( )
| A、32 | B、31 | C、16 | D、15. |
设f(x)=2a2x-1,g(x)=x2+ax-1,若f(1)=g(1)且a≠1,则2a÷a2=( )
A、±2
| ||||
B、±
| ||||
C、2
| ||||
D、
|
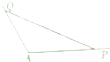 如图,角A为钝角,且sinA=
如图,角A为钝角,且sinA=