题目内容
画出f（x）=|x-2|-|x+1|图象，求值域．
考点：函数的图象
专题：函数的性质及应用
分析：可将定义域分成（-∞，-1]，（-1，2]，（2，+∞）三个区间来讨论，再将所得三个区间的值域取并集即可．
解答：
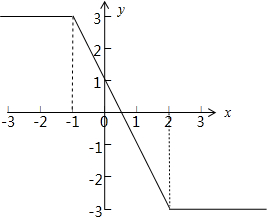解：可将定义域分成（-∞，-1]，（-1，2]，（2，+∞）三个区间来讨论，
①当x≤-1时，f（x）=2-x+x+1=3，
②当-1＜x≤2时，f（x）=-（x-2）-x-1=-2x+1，
f（x）是减函数，值域为[-3，3），
③当x＞2时，f（x）=（x-2）-（x+1）=-3；
函数的图象为：
综上所述，函数f（x）的值域为[-3，3]．
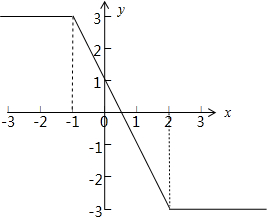解：可将定义域分成（-∞，-1]，（-1，2]，（2，+∞）三个区间来讨论，①当x≤-1时，f（x）=2-x+x+1=3，
②当-1＜x≤2时，f（x）=-（x-2）-x-1=-2x+1，
f（x）是减函数，值域为[-3，3），
③当x＞2时，f（x）=（x-2）-（x+1）=-3；
函数的图象为：
综上所述，函数f（x）的值域为[-3，3]．
点评：本题很好的体现了分类讨论思想，另外在解题时注意负号，虽然简单，有时也容易出错．
练习册系列答案
相关题目
设点A，B分别在直线3x-y+5=0和3x-y-13=0上运动，线段AB的中点M恒在圆x2+y2=8内，则点M的横坐标的取值范围为（ ）
A、（
| ||
B、（-2，-
| ||
C、（2，
| ||
D、（-
|