题目内容
从6名男生和2名女生中选出3名志愿者,其中至少有1名女生的选法共有 种.
考点:排列、组合及简单计数问题
专题:计算题,排列组合
分析:从6名男生和2名女生中选出3名志愿者,共有C83种结果,其中包括不合题意的没有女生的选法,其中没有女生的选法有C63用所有的结果是减去不合题意的数字,得到结果.
解答:
解:从6名男生和2名女生中选出3名志愿者,
共有C83种结果,其中包括不合题意的没有女生的选法,
其中没有女生的选法有C63
∴至少有1名女生的选法有C83-C63=56-20=36
故答案为:36.
共有C83种结果,其中包括不合题意的没有女生的选法,
其中没有女生的选法有C63
∴至少有1名女生的选法有C83-C63=56-20=36
故答案为:36.
点评:本题考查排列组合简单的计数原理的应用,本题是一个典型的问题,可以分类来解,即有一个女生和有两个女生两种情况,注意做到不重不漏.

练习册系列答案
相关题目
 运行如图所示的程序框图,输出A,B,C的一组数据为
运行如图所示的程序框图,输出A,B,C的一组数据为 | 3 |
| A、垂直、相切 |
| B、平行、相交 |
| C、垂直、相离 |
| D、平行、相切 |
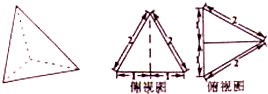 某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是
某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是