题目内容
在直角坐标平面内,以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知直线l的参数方程为
(t为参数),圆C的极坐标方程为ρ+2cosθ=0.
(Ⅰ)将直线l的参数方程化为普通方程,圆C的极坐标方程化为直角坐标方程;
(Ⅱ)求圆C上的点到直线l的距离的最小值.
|
(Ⅰ)将直线l的参数方程化为普通方程,圆C的极坐标方程化为直角坐标方程;
(Ⅱ)求圆C上的点到直线l的距离的最小值.
考点:直线的参数方程,简单曲线的极坐标方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)将直线l的参数方程的参数t消去即可求出直线的普通方程,利用极坐标转化成直角坐标的转换公式求出圆的直角坐标方程;
(Ⅱ)求出圆心C(0,-2)到直线x+y-1=0的距离,即可得到圆C上的点到直线的距离的最小值.
(Ⅱ)求出圆心C(0,-2)到直线x+y-1=0的距离,即可得到圆C上的点到直线的距离的最小值.
解答:
解:(Ⅰ)直线l的参数方程为
(t为参数),消去参数t,
得直线l的普通方程为
x+y-3
=0,
ρ+2sinθ=0,两边同乘以ρ得ρ2+2ρcosθ=0,得⊙C的直角坐标方程为(x+1)2+y2=1;
(Ⅱ)因为圆心为C(-1,0),
所以点C到直线的距离为d=
=2
,
所以圆上的点到直线距离的最小值为2
-1.
|
得直线l的普通方程为
| 3 |
| 3 |
ρ+2sinθ=0,两边同乘以ρ得ρ2+2ρcosθ=0,得⊙C的直角坐标方程为(x+1)2+y2=1;
(Ⅱ)因为圆心为C(-1,0),
所以点C到直线的距离为d=
|-
| ||||
| 2 |
| 3 |
所以圆上的点到直线距离的最小值为2
| 3 |
点评:本题考查极坐标方程与直角坐标方程,参数方程与普通方程的互化,考查点线距离公式的运用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
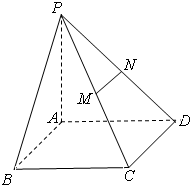 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,M、N分别是PC、PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是矩形,M、N分别是PC、PD的中点.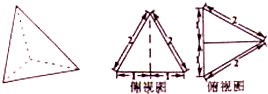 某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是
某三棱锥及其侧视图、俯视图如图所示.则该三棱锥的表面积是