题目内容
已知曲线C：f（x）=x3．求曲线C上横坐标为1的点处的切线方程．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求出函数的导数，利用导数的几何意义即可得到切线方程．
解答：
解：∵f（x）=x3，
∴f'（x）=3x2，
∴将x=1代入曲线C的方程，得y=1，
∴切点的坐标为（1，1）．
又∵切线的斜率k=f'（1）=3×12=3，
∴过点（1，1）的切线的方程为y-1=3（x-1），
即3x-y-2=0．
∴f'（x）=3x2，
∴将x=1代入曲线C的方程，得y=1，
∴切点的坐标为（1，1）．
又∵切线的斜率k=f'（1）=3×12=3，
∴过点（1，1）的切线的方程为y-1=3（x-1），
即3x-y-2=0．
点评：本题主要考查函数切线的求解，利用导数的几何意义求出切线斜率是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
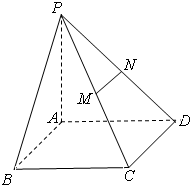如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是矩形，M、N分别是PC、PD的中点．