题目内容
已知数列{an}为等差数列,{bn}为等比数列,且满足:a1000+a1013=π,b1b14=-2,则tan
=( )
| a1+a2012 |
| 1-b7b8 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、
|
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:由已知得a1+a2012=π,b7b8=-2,由此能求出tan
=tan
=
.
| a1+a2012 |
| 1-b7b8 |
| π |
| 3 |
| 3 |
解答:
解:∵数列为等差数列,a1000+a1013=π,
∴a1+a2012=π
∵{bn}为等比数列,b1b14=-2,
∴b7b8=-2,
∴tan
=tan
=
.
故选:D.
∴a1+a2012=π
∵{bn}为等比数列,b1b14=-2,
∴b7b8=-2,
∴tan
| a1+a2012 |
| 1-b7b8 |
| π |
| 3 |
| 3 |
故选:D.
点评:本题考查正切值的求法,是中档题,解题时要注意等差数列和等比数列的性质的合理运用.

练习册系列答案
相关题目
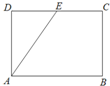
如图,在矩形ABCD中,AB=2,BC=
,E是CD的中点,那么
•
=( )
| 3 |
| AE |
| DC |

| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,有xf′(x)<f(-x)成立.(其中f′(x)是f(x)的导函数),若a=
f(
),b=f(1),c=log2
f(log2
)则a,b,c的大小关系是( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、a>b>c |
| B、c>b>a |
| C、b>a>c |
| D、c>a>b |
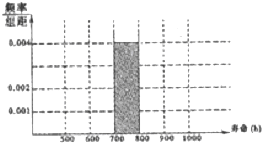 对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表:
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表: