题目内容
20．设0＜x＜1，0＜y＜1，且x≠y，则x+y，2$\sqrt{xy}$，x2+y2，2xy中最大的一个是x+y．分析 由题意和基本不等式可得x+y＞2$\sqrt{xy}$，x2+y2＞2xy，只需由不等式的性质比较x+y和x2+y2的大小即可．
解答 解：由题意和基本不等式可得x+y＞2$\sqrt{xy}$，x2+y2＞2xy，
又∵0＜x＜1，0＜y＜1，∴x2＜x，y2＜y，
∴x2+y2＜x+y，
∴最大的一个为x+y，
故答案为：x+y．
点评 本题考查基本不等式比较式子的大小，属基础题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
8．下列函数f（x），g（x）表示同一个函数的是（ ）
| A． | f（x）=$\frac{{x}^{2}-1}{x-1}$与g（x）=x+1 | B． | f（x）=lnex与g（x）=elnx | ||
| C． | f（x）=|x|与g（x）=$\sqrt{{x}^{2}}$ | D． | f（x）=$\sqrt{x-1}$•$\sqrt{x+1}$与g（x）=$\sqrt{{x}^{2}-1}$ |
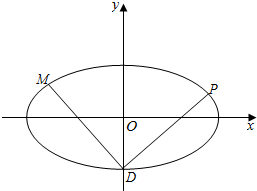如图，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率e=$\frac{2\sqrt{2}}{3}$，椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$，椭圆C的下顶点为D．
4．抛物线y2=8x的焦点为F，点P（x，y）为该抛物线上的动点，又已知点A（-2，0），则$\frac{|PA|}{|PF|}$的取值范围是（ ）
| A． | [3，+∞） | B． | （1，2] | C． | [1，4] | D． | [1，$\sqrt{2}$] |