题目内容
18.已知集合$A=\{x|\frac{5-x}{x+1}≥1\}$,集合B={x||x-m|≤2},若A∩B≠∅,求m的取值范围.分析 求出A中不等式的解集确定出A,求出B中不等式的解集表示出B,根据A与B的交集不为空集,确定出m的范围即可.
解答 解:由A中不等式变形得:1+$\frac{x-5}{x+1}$≤0,即$\frac{2x-4}{x+1}$≤0,
解得:-1<x≤2,即A=(-1,2],
由B中不等式解得:-2≤x-m≤2,即m-2≤x≤m+2,
∴B=[m-2,m+2],
∵A∩B≠∅,
∴m+2
∴-1≤m-2≤2或-1<m+2≤2,
解得:1≤m≤4或-3<m≤0.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
13.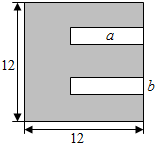 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |
3.已知x,y满足约束条件,$\left\{\begin{array}{l}{y≤1}\\{x+y-2≥0}\\{x-y-1≤0}\end{array}\right.$,则目标函数z=2x-y的最大值为( )
| A. | 1 | B. | 3 | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
7.用反证法证明“a+b$\sqrt{2}$(a、b∈Z)是无理数”时,假设正确的是( )
| A. | 假设$\sqrt{2}$是有理数 | B. | 假设b$\sqrt{2}$(b∈Z)是有理数 | ||
| C. | 假设a+$\sqrt{2}$(a∈Z)是有理数 | D. | 假设a+b$\sqrt{2}$(a、b∈Z)是有理数 |
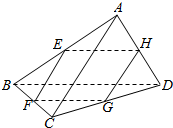 如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.
如图所示,在三棱锥A-BCD中,E,F,G,H分别是棱AB,BC,CD,DA的中点,则当AC,BD满足条件AC=BD时,四边形EFGH为菱形.