题目内容
3.已知曲线C1的参数方程是$\left\{\begin{array}{l}{x=5cosφ}\\{y=\frac{5\sqrt{22}}{22}sinφ}\end{array}\right.$(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立坐标系,曲线C2的极坐标方程是psin($θ-\frac{π}{6}$)=0,且曲线C1与曲线C2在第一象限的交点为A,长方形ABCD的顶点都在C1上(其中A,B,C,D依逆时针次序排列)求点A,B,C,D的直角坐标.分析 求出曲线C1、C2的普通坐标方程,联立方程组得A($\sqrt{3}$,1),由此利用椭圆的对称性能求出点A,B,C,D的直角坐标.
解答 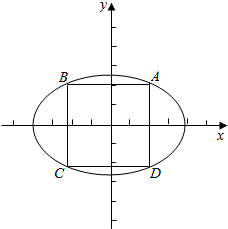 解:∵曲线C1的参数方程是$\left\{\begin{array}{l}{x=5cosφ}\\{y=\frac{5\sqrt{22}}{22}sinφ}\end{array}\right.$(φ为参数),
解:∵曲线C1的参数方程是$\left\{\begin{array}{l}{x=5cosφ}\\{y=\frac{5\sqrt{22}}{22}sinφ}\end{array}\right.$(φ为参数),
∴曲线C1的普通方程是$\frac{{x}^{2}}{25}+\frac{22{y}^{2}}{25}$=1,
∵曲线C2的极坐标方程是ρsin($θ-\frac{π}{6}$)=0,
即$ρsinθcos\frac{π}{6}-ρcosθsin\frac{π}{6}$=0,
∴$\frac{\sqrt{3}}{2}ρsinθ-\frac{1}{2}ρcosθ=0$,
∴曲线C2的普通坐标方程$\frac{\sqrt{3}}{2}y-\frac{1}{2}x=0$,
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{15}+\frac{22{y}^{2}}{25}=1}\\{\frac{\sqrt{3}}{2}y-\frac{1}{2}x=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\sqrt{3}}\\{y=-1}\end{array}\right.$,
∵曲线C1与曲线C2在第一象限的交点为A,∴A($\sqrt{3}$,1),
∵长方形ABCD的顶点都在C1上(其中A,B,C,D依逆时针次序排列),
∴A($\sqrt{3}$,1),B(-$\sqrt{3}$,1),C(-$\sqrt{3}$,-1),D($\sqrt{3}$,-1).
点评 本题考查长方形的四个顶点的直角坐标的求法,是基础题,解题时要认真审题,注意极坐标、直角坐标互化公式的合理运用.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | 0 | B. | 2 | C. | 0或2 | D. | 1或2 |
| A. | 一条直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
①若l⊥m,m⊥n,则l∥n;
②若m⊥α,n⊥β,α⊥β,则m⊥n;
③若m∥α,n∥β,α∥β,则m∥n;
④若l与α、β所成角相等,且m⊥α,n⊥β,则l与m、n所成角相等.
其中真命题是( )
| A. | ①和② | B. | ①和③ | C. | ②和④ | D. | ①和④ |
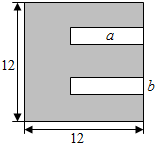 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |