题目内容
7.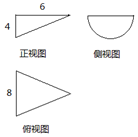 某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形,各边的长度如图所示,则此几何体的体积是16π,表面积是$24+(8+4\sqrt{13})π$.
某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形,各边的长度如图所示,则此几何体的体积是16π,表面积是$24+(8+4\sqrt{13})π$.
分析 由已知可得:该几何体是一个以侧视图为底面的半圆锥,代入锥体体积和表面积公式,可得答案.
解答 解:由已知可得:该几何体是一个以侧视图为底面的半圆锥,
底面直径为8,故底面半径r=4,故底面面积S=$\frac{1}{2}π•{4}^{2}$=8π,
高h=6,
故体积V=$\frac{1}{3}Sh$=16π,
母线l=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
故表面积S=$\frac{1}{2}π•{4}^{2}$+$\frac{1}{2}π•4×2\sqrt{13}$+$\frac{1}{2}$×8×6=$24+(8+4\sqrt{13})π$,
故答案为:16π,$24+(8+4\sqrt{13})π$.
点评 本题考查的知识点是圆锥的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
17.已知x,y∈R,满足x2+2xy+4y2=6,则z=x+y的取值范围为( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | [-$\sqrt{2}$,$\sqrt{6}$] | C. | [-$\sqrt{6}$,$\sqrt{6}$] | D. | [-$\sqrt{6}$,$\sqrt{2}$] |
15.设全集U=R,集合A={x|x2-1<0},B={x|x(x-2)>0},则A∩(∁uB)=( )
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
2.点P为直线$y=\frac{3}{4}x$上任一点,F1(-5,0),F2(5,0),则下列结论正确的是( )
| A. | ||PF1|-|PF2||>8 | B. | ||PF1|-|PF2||=8 | C. | ||PF1|-|PF2||<8 | D. | 以上都有可能 |
19.已知函数$f(x)=\left\{\begin{array}{l}{x^2}+2x-3,x≤0\\ lnx-a,x>0\end{array}\right.({a∈R})$,若关于x的方程f(x)=k有三个不相等的实数根,则实数k的取值范围是( )
| A. | (-∞,-4) | B. | [-4,-3] | C. | (-4,-3] | D. | [-3,+∞) |
17.设m,n是不同的直线,α,β是不同的平面,下列命题中正确的是( )
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m∥α,n⊥β,m∥n,则α⊥β | ||
| C. | 若m∥n,m∥α,n∥β,则α∥β | D. | 若m?α,n?α,m∥β,n∥β,则α∥β |