题目内容

2．点P为直线$y=\frac{3}{4}x$上任一点，F1（-5，0），F2（5，0），则下列结论正确的是（　　）
A．||PF1|-|PF2||＞8B．||PF1|-|PF2||=8C．||PF1|-|PF2||＜8D．以上都有可能

分析 运用双曲线的定义，可得双曲线方程和渐近线方程，即可得到结论．

解答 解：若||PF1|-|PF2||=8，
则点P的轨迹是以F1（-5，0），F2（5，0）为焦点的双曲线，
其方程为$\frac{x^2}{16}-\frac{y^2}{9}=1$．因为直线$y=\frac{3}{4}x$是它的渐近线，整条直线在双曲线的外面，
因此有||PF1|-|PF2||＜8．
故选：C．

点评 本题考查双曲线的定义、方程和性质，考查运算能力，属于中档题．

练习册系列答案
相关题目
12．设a=0.32，b=20.3，c=log25，d=log20.3，则a，b，c，d的大小关系是（　　）
A．d＜b＜a＜cB．d＜a＜b＜cC．b＜c＜d＜aD．b＜d＜c＜a
13．关于x的不等式x2-ax-6a2＞0（a＜0）的解集为（-∞，x1）∪（x2，+∞），且x2-x1=5$\sqrt{2}$，则a的值为（　　）
A．-$\sqrt{5}$B．-$\frac{3}{2}$C．-$\sqrt{2}$D．-$\frac{\sqrt{5}}{2}$
10．直线l：y-1=k（x-1）和圆x2+y2-2x=0的位置关系是（　　）
A．相离B．相切或相交C．相交D．相切
17．$f（x）={log_{\frac{1}{2}}}（3-2x-{x^2}）$的增区间为（-1，1）．
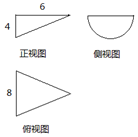7．某几何体的三视图是如图所示的直角三角形、半圆和等腰三角形，各边的长度如图所示，则此几何体的体积是16π，表面积是$24+（8+4\sqrt{13}）π$．
14．定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数$f（x）=\frac{1}{3}{x^3}+a{x^2}+x+1$，
（1）当$a=-\frac{5}{3}，D=[-1，3]$时，求函数f（x）在D上的上界的最小值；
（2）记函数g（x）=f′（x），若函数$y=g[{（\frac{1}{2}）^x}]$在区间D=[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．
11．某学校为了调查大声朗读对学生的记忆是否有明显的促进作用，把200名经常大声朗读的学生与另外200名经常不大声朗读的学生的日常记忆情况作记载后进行比较，提出假设H0：“经常大声朗读对记忆没有明显的促进作用”，利用2×2列联表计算得K2≈3.918，经查对临界值表知P（K2≥3.841）≈0.05．根据比较结果，学校作出了以下的四个判断：
p：有95%的把握认为“经常大声朗读对记忆有明显的促进作用”；
q：若某学生经常大声朗读，那么他有95%的可能记忆力很好；
r：经常大声朗读的学生中，有95%的学生的记忆有明显的促进；
s：经常大声朗读的学生中，只有5%的学生的记忆有明显的促进．
则下列结论中，正确结论的序号是①④．（把你认为正确的命题序号都填上）
①p∧非q　②非p∧q  ③（非p∧非q）∧（r∨s）　④（p∨非r）∧（非q∨s）
12．已知函数f（x）=3x+x，g（x）=x3+x，h（x）=log3x+x的零点依次为a，b，c，则（　　）
A．c＜b＜aB．a＜b＜cC．c＜a＜bD．b＜a＜c

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网